y' = 12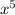
+ sinx
Объяснение:
Для нахождения производной, воспользуемся двумя формулами:
1) при нахождении производной разности, нужно помнить, что производная разности равна разности производных. (u - v)' = u' - v'. Если немного запутано, то когда будешь смотреть пример, то, думаю, поймёшь. 2) (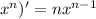
3) (cosx)' = - sinx
у = 2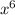
- cosx
y' = (2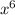 - cosx)' = (2 · 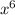)' - (cosx)' = 2 · (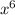)' - (cosx)' = 2 · 6 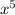- (-sinx) = 12 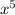+ sinx
Попробую ещё немного объяснить:
Как получить производную от 2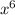
Сначала перепишем за знак производной константу 2 (2 - число, которое не может просто взять и измениться само по себе - константа) и поставим знак умножения, дальше нас интересует нахождение производной от 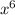. По формуле, которую я записала выше, мы можем увидеть, что показатель степени 6 мы записываем перед х (становится множителем), но х не остаётся без показателя степени, по формуле записано n - 1, то есть в нашем случае это 6 - 1 ( = 5), то есть х становится в 5й степени.
С косинусом даже легче: производная косинуса (по формуле) равна синусу, но обязательно со знаком минус, т.е. - sinx
Третий момент, на который нужно обратить внимание, - то, что перед косинусом первоначально был минус. При нахождении производной получается - (-sinx), если перед скобкой стоит минус, то знак в скобках меняется, поэтому в ответе становится + sinx.
Если ещё есть вопросы, задавай в комментариях.
а) Отметьте на координатной плоскости точкиA(1;5), B(3;6), C(2;13), D(5;5),E (7; 8), F (12; 4). Соедините их последовательно отрезками AB, BC, CD, DE, EF и FA и найдите площадь получившейся фигуры.
б) При каких значениях k прямая y = kx имеет с данной фигурой хотя бы одну общую точку?
Вторая задача:
Биссектриса PC и медиана QA треугольника PQR взаимно перпендикулярны и пересекаются в точке F . Площадь треугольника PQR равна 40. Найдите площадь треугольника FPQ.
Если можно, ответы в комментарии :)