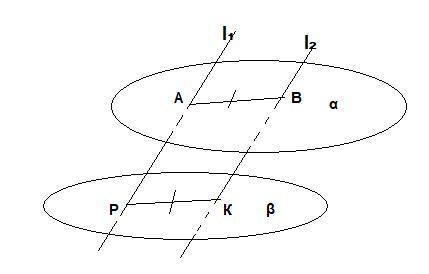
Параллельные прямые l1 и l2 пересекают плоскость альфа в точках А и В.Доказать,что любая плоскость,параллельная плоскости альфа,пересекает прямые l1 и l2 в точках,расстояние между которыми равно АВ.
Объяснение:
Т.к. l₁║l₂ то через через эти прямые можно провести плоскость единственным образом.
По т. " Если 2-е параллельные плоскости пересечены третьей , то линии их пересечения параллельны " → АВ║РК .
И АР║ВК , т.к лежат на параллельных прямых, ⇒АРКВ- параллелограмм и у него противоположные стороны равны АВ=РК.
АВ = √((Хв-Ха)²+(Ув-Уа)²) = √40 = 6.32455532,
BC = √((Хc-Хв)²+(Ус-Ув)²) = √40 = 6.32455532,
AC = √((Хc-Хa)²+(Ус-Уa)²) = √16 = 4.
Из этого расчёта видно, что треугольник равнобедренный.
Периметр равен 16,64911064.
2) МЕДИАНЫ ТРЕУГОЛЬНИКА Медиана АM1 из вершины A: Координаты M1(3; -1) Длина AM1 = 4.24264068711928 Медиана BM2 из вершины B: Координаты M2(2; 2) Длина BM2 = 6 Медиана CM3 из вершины C: Координаты M3(1; -1) Длина CM3 = 4.24264068711928
Длины средних линий:
А₁В₁ = АВ/2 = 3.16227766,
В₁С₁ = ВС/2 = 3.16227766,
А₁С₁ = АС/2 = 2.