3.Сторона прямоугольника 4 см, а площадь - 25 см“. Найти вторую сторону.

a) 5,5 CM

в) 16 см

г) 6,25 см

6) 5 CM

4.Диагонали ромба 2 см и 6 см. Найти площадь ромба.

a) 6 cm

б) 6,5 см

B) 7,5 cm

r) 8 cm

5. Средняя линия трапеции 6 см, а высота - 3 см. Найти площадь трапеции.

a) 9 cM

6) 18 CM

г) 27 см

в) 36 см

6. Площадь треугольника 18 см". Найти высоту треугольника, если она в два раза меньше стороны, к которой она проведена.

7.Параллелограмм имеет такую же площадь, что и квадрат с периметром 32 см.

Высота параллелограмма равна 4 см. Найти сторону параллелограмма, к которой проведена эта высота.

8.Радиус окружности, вписанной в трапецию, равна 4 см. Боковые стороны равны 11 см и 14 см. Найти площадь трапеции.

✊

👇

Открыть все ответы

Ответ:

lianochkaya14

28.05.2021

1) Расположим куб в системе координат так, как показано на рисунке. Точка А - совпадаем с началом координат. Тогда координаты вершин
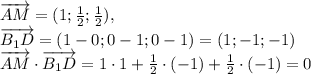
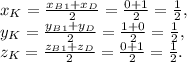
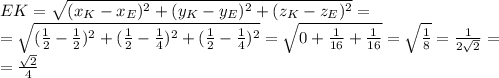
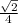
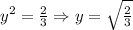
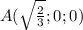
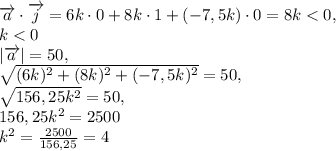
А(0;0;0) ; В(0;1:0) ; С(1; 1; 0) ; D(1; 0; 0) ; В₁(0;1;1)
Координаты точки М (1; 1/2; 1/2)
Координаты векторов
$\overrightarrow{AM}=(1;
 \frac{1}{2}; \frac{1}{2} ), \\ \overrightarrow{B _{1}D 
}=(1-0;0-1;0-1)=(1;-1;-1) \\ \overrightarrow{AM}\cdot \overrightarrow{B 
_{1}D} =1\cdot1+ \frac{1}{2}\cdot(-1)+ \frac{1}{2}\cdot(-1)=0$
Скалярное произведение равно 0, значит векторы ортогональны, прямые AM и B₁D перпендикулярны
Найдем координаты середины отрезка В₁D - точки K
$x
 _{K}= \frac{x_B _{1}+x_D }{2}= \frac{0+1}{2}= \frac{1}{2}, \\ y _{K}=
 \frac{y_B _{1}+y_D }{2}= \frac{1+0}{2}= \frac{1}{2}, \\ z _{K}= 
\frac{z_B _{1}+z_D }{2}= \frac{0+1}{2}= \frac{1}{2}.$
K(1/2; 1/2;1/2)
Найдем координаты середины отрезка АМ - точки Е
$x
 _{E}= \frac{x_A +x_M }{2}= \frac{0+1}{2}= \frac{1}{2}, \\ y _{E}= 
\frac{y_A +y_M }{2}= \frac{1+ \frac{1}{2} }{2}= \frac{1}{4}, \\ z _{E}= 
\frac{z_A+z_M }{2}= \frac{0+ \frac{1}{2} }{2}= \frac{1}{4}.$
E=(1/2; 1/4:1/4)
$EK=
 \sqrt{(x_K-x_E) ^{2}+(y_K-y_E) ^{2} +(z_K-z_E) ^{2}} = \\ =\sqrt{( 
\frac{1}{2} - \frac{1}{2} ) ^{2}+( \frac{1}{2} - \frac{1}{4} ) ^{2} +( 
\frac{1}{2} - \frac{1}{4} ) ^{2}}= \sqrt {0+ \frac{1}{16}+\frac{1}{16} 
}= \sqrt{ \frac{1}{8} }= \frac{1}{2 \sqrt{2} }= \\ = \frac{ \sqrt{2} 
}{4}$
ответ. 1) прямые АМ и В₁D перпендикулярны, угол между ними 90°.2) расстояние между серединами отрезков АМ и В₁D равно $\frac{ 
\sqrt{2} }{4}$

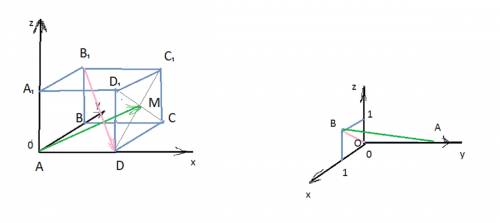
Задача 2. ( см. рис. 2)
В грани ОХZ - квадрат, все стороны которого 1. Диагональ квадрата ОВ имеет длину √2 и легко находится по теореме Пифагора 1²+1²=2²
В прямоугольном треугольнике АВО угол АВО равен 30°, угол АОВ равен 90°, так как ось оу перпендикулярна плоскости ОХZ.
В прямоугольном треугольнике против угла в 30° катет в два раза меньше гипотенузы. Пусть ОА=y, тогда АВ=2y
По теореме Пифагора АВ²=АО²+ВО²
(2y)²=y²+(√2)² ⇒ 3y²=2 ⇒ $y^{2} = \frac{2}{3}\Rightarrow y= \sqrt{ \frac{2}{3} }$
ответ. $A( \sqrt{ \frac{2}{3} };0;0)$

Задача 3.
Так как векторы а и b коллинеарны, то их координаты пропорциональны.
Вектор a имеет координаты (6k; 8k;-7,5k), где k- коэффициента пропорциональности
Так как угол между векторами a и j - тупой, значит их скалярное произведение отрицательно.
Координаты вектора j - (0;1:0)
Найдем скалярное произведение
$
 \overrightarrow{a}\cdot 
\overrightarrow{j}=6k\cdot0+8k\cdot1+(-7,5k)\cdot0=8k$
Так как k<0, то к=-2
ответ. Вектор a имеет координаты (6·(-2); 8·(-2);-7,5·(-2)=(-12; -16; 15)

Решить, ! 1. в кубе abcda1b1c1d1 длина ребра равна 1. m - центр грани dd1c1c. используя метод коорди