Вступление:
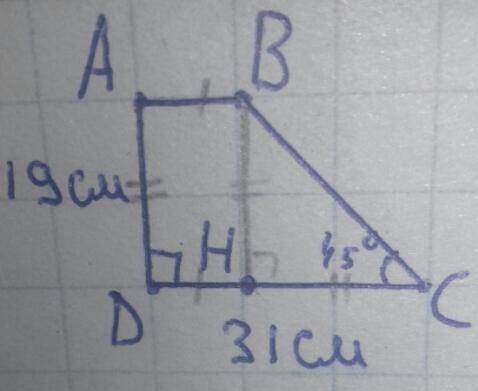
Пусть в прямоугольной трапеции ABCD, AB и CD основания, а ∠D прямой. Тогда AD меньшая боковая сторона (как расстояние между параллельными отрезками AB и CD), то есть AD=19см. По построению DC большое основание, поэтому по условию DC=31см. Острые углы при большом основании, ∠C=45° т.к. ∠D=90°.
H∈DC, BH⊥DC ⇒ BH=AD=19см.
В прямоугольном ΔBHC:
∠C=45°, ∠H=90° ⇒ ∠B=45°⇒ HC=BH=19см.
DH=DC-HC=31-19=12см.
В четырёхугольнике ABHD:
∠D=90°, ∠H=90° и ∠A=90°, ∠B=90° т.к. AB║DH, ведь H∈DC и AB║DC.
Получается ABHD - прямоугольник, поэтому AB=HD, HD=12см ⇒ AB=12см.
AB мень. осн. т.к. CD - большее.
Меньшее основание равно 12см.
A(0;0;0) ; B(0 ;1; 0) ; C(1;1;0) ; D(1;0;0) ;
A₁(0;0;1) ;B₁(0 ;1; 1) ; C₁(1;1;1) ; D₁(1;0;1) .
AD₁(1;0;1) и BA₁(0 ; -1;1).
Скалярное произведение
AD₁. BA₁ = 1*0 +0*(-1) +1*1 =1 ;
AD₁. BA₁ =|AD₁|. |BA₁|*cos(AD₁^BA₁) (определение скалярного произведения) ;
* * * модуль(длина) векторов |AD₁| =√(1²+0²+1²) =√2 ; |BA₁| = √(0²+(-1)²+1²) =√2 * * *
√2*√2cosα =1 ;
cosα =1/2.
α =60°.
BD(1; -1; 0) и DC₁(0;1;1).
BD*DC₁=1*0 +(-1)*1+0*1= -1.
√2*√2 cosβ = - 1 ;
cosβ = -1/2 ;
β = 120°.