Задача 1: ( доказательство первого свойства):
Дано: АВС, т. М АВ, М – середина АВ, СМ = ВМ = МА
Обозначим углы 1, А – 4, ВСМ – 2, АСМ – 3
Доказать: АВС – прямоугольный.
Доказательство: 1). СВМ - р/б., значит, 1 = …,
СМА – р/б., значит, 3 = …
2). 1 + 2 + 3 + 4 = , т.к. В + ВСА + А = (по теореме о сумме углов треугольника) 2 (2 + 3) = ,
2 + 3 = …,т.е. ВСА = …
Задача 2. Дано: АВС, С = , В = , т. М – середина АВ.
Найти: МСА.
Задача 3. Дано: АВС, С = , т. D – середина АС, отр. BD = AD = CD.
Найти: А, АВС.
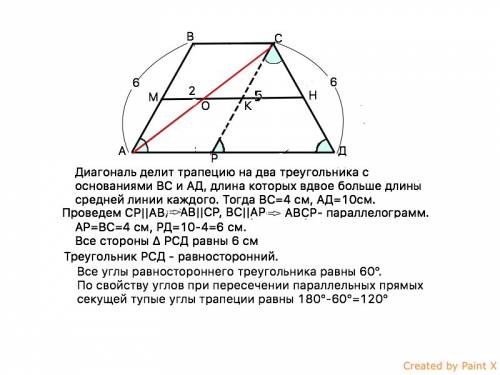
ВС=2*2=4 см, а АD=2*5=10 см.
Трапеция равнобедренная, значит высота ВН, проведенная у большему основанию, делит его на два отрезка, большй из которых равен полусумме оснований, а меньший - их полуразности.
Значит АН=(10-4):2=3 см. В прямоугольном треугольнике АВН катет АН равен половине гипотенузы АВ, следовательно, угол, против которого лежит этот катет (<ABH), равен 30° (свойство).
В прямоугольном треугольнике сумма острых углов равна 90°, значит
<A=90°-30°=60°.
Углы трапеции, прилежащие к боковой стороне, в сумме равны 180°.
Значит угол В=180°-60°=120°.
Так как трапеция равнобедренная, углы при основаниях равны.
ответ: <A=<D=60°, <B=<C=120°.