смотри ниже
Объяснение:
2. уравнение прямой: y=kx+C; Эта прямая пересекает ось 0Y в точке C, а тангенс угла между этой прямой и осью 0X равен k.
Если прямая параллельна оси 0X, то угол между прямой и этой осью равен нулю. Тангенс нуля тоже равен нулю, значит k=0. Получаем уравнение прямой, параллельной оси 0X: y=0*x+C; то есть y=C
Значит в задании 2. уравнение прямой имеет вид y=-2
3. подставляем значение абсциссы (x=1) в уравнение и находим нужные точки.
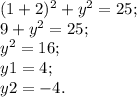
Первая точка (1;4) вторая (1;-4)
4. уравнение окружности
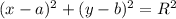
Где (a;b) координаты центра окружности.
В данном уравнении 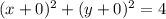
центр окружности находится в начале координат (0;0), значит наша прямая совпадает с осью 0Y и описывается уравнением x=0
5. прямая y=8 параллельна оси абсцисс 0X, значит диаметр окружности равен 8, а радиус равен 4.
Объяснение:
Центром тяжести треугольника является точка пересечения его медиан. Пусть в треугольнике АВС медиана ВТ, точка М- центр тяжести,, КЕ проходит через М и параллельна АС.
В треугольниках АВС и КВЕ угол при вершине В общий, соответственные углы при пересечении АС и КЕ боковыми сторонами равны ( КЕ||АС, АВ и СВ - секущие). Следовательно, ∆ КВЕ подобен ∆АВС. По свойству медиан ВМ:МТ=2:1, ⇒ ВЕ:ЕС=2:1, а k=ВЕ:ВС=2/3 Отношение площадей подобных фигур равно квадрату коэффициента подобия.
Ѕ(КВЕ):Ѕ(АВС)=k²=4/9.
Примем коэффициент отношения площадей равным а. Тогда Ѕ(АКЕС)=Ѕ(АВС)-Ѕ(КВЕ)=9а-4а=5а ⇒ Ѕ(КВЕ):Ѕ(АКЕС)=4а:5а=4/5

Фото
Объяснение: