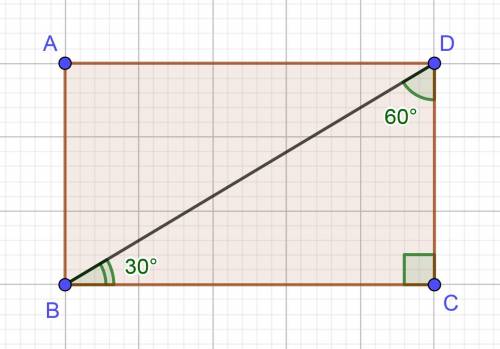
Нехай дано прямокутник ABCD, BD — діагональ, DC = 10 см, ∠BDC = 60°.
Р-мо BDC:
∠BCD = 90° — як кут прямокутника, отже ΔBDC — прямий, ∠BDC = 60° — за умовою, тоді ∠DBC за теоремою про суму кутів трикутника буде дорівнювати:
∠DBC = 180°−90°−60° = 30°.
По властивості катета, який лежить напроти кута 30°, гіпотенуза трикутника буде рівна:
BD = 2*DC = 2*10 = 20 (cm)
Знайдемо інший катет за т. Піфагора:
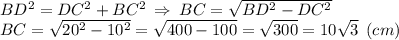
Підставимо значення у формулу площі прямокутника:

Відповідь: Площа прямокутника рівна 100√3 см² або приблизно 173,2 см².
Объяснение:
^ - возведение в степень
1. Площадь параллелограмма равна произведению стороны и проведённой к ней высоты. Значит, S = BC * BH.
S = 20см * 5см = 100см^2
2. Площадь прямоугольного треугольника равна половине произведения катетов. Так как в условии сказано, что угол B = 90, то можно сказать, что проведённые из этого угла стороны BK и BD - катеты по определению. Значит, S = (BK * BD) / 2.
S = (50см * 2см) / 2 = 50см^2
3. По теореме Пифагора: AC^2 + AB^2 = CB^2.
AC^2 = BC^2 - AB^2.
AC^2 = 32.
AC = 4V2 (V - квадратный корень)
4. По формуле Герона: S = Vp(p-a)(p-b)(p-c), где p - полупериметр. Он равен 16 см. Вычисляем площадь. S = V2304
S = 48
Теперь, зная, что площадь треугольника равна половине произведения высоты на сторону, вычисляем высоту/ S = (a * b) / 2
Получаем три высоты: 9,6см; 9,6см; 8см.
5. Площадь ромба равна половине произведения диагоналей (мало где говорится, но это можно вывести из формул площадей других фигур) S = (5см * 12см) / 2 = 30см^2.
Диагонали ромба делят его на 4 равных прямоугольных треугольника, катеты которых равны половинам диагоналей. Т.е. если взять один из таких треугольников, два его катета будут равны 2,5см и 6см. Теперь вычисляем всё по той же теореме Пифагора гипотенузу или же сторону ромба. Она будет равна 6,5 см