∠CBD = arcsin(3√7/14) ≈ arcsin(0,567) => ∠CBD ≈ 34,6°.
Объяснение:
Высота призмы - отрезок ОН1 по условию (так как он перпендикулярен основаниям). =>
АВ=ВС=АС=ОН1.
Основания призмы - правильные треугольники. Следовательно, центр основания АВС - точка О лежит на пересечении высот(медиан, биссектрис) этого треугольника.
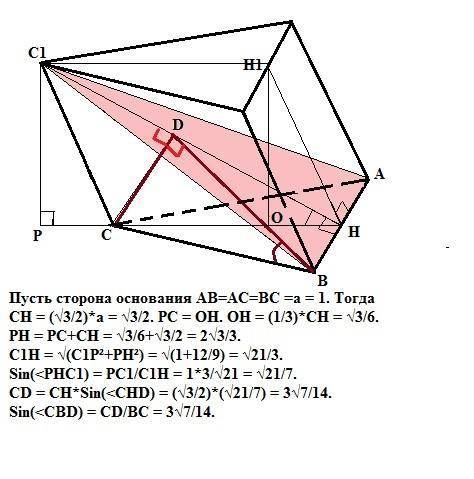
Проведем высоту СН основания и опустим перпендикуляр С1Р на плоскость, содержащую основание АВС. Точка Р принадлежит продолжению прямой НС, так как РН - проекция С1Н на плоскость, содержащую основание АВС.
Прямоугольные треугольники ОН1Н и РС1С равны по катету С1Р=Н1О и гипотенузе С1С = Н1Н.
=> PC = OH = (1/3)*СН (так как СН - медиана и делится в отношении 2:1, считая от вершины).
СН = (√3/2)*а, где а - сторона треугольника. Пусть сторона основания равна 1. Тогда
СН = √3/2, а РН = РС+СН = (1/3)*(√3/2)+√3/2 = 2√3/3.
В прямоугольном треугольнике РС1Н по Пифагору
С1Н = √(С1Р²+РН²) = √(1+12/9) = √21/3.
Прямоугольные треугольники ∆СDН ~ ∆C1PH по острому углу С1НР.
Из подобия: СD/C1P = CH/C1H => CD = CH*C1P/C1H =>
CD = (√3/2)*1/(√21/3) = 3√7/14.
Sin(∠CBD) = CD/CB = 3√7/14.
∠CBD = arcsin(3√7/14) ≈ arcsin(0,567) => ∠CBD ≈ 34,6°.
1) Проведём прямую a.
2) Построим перпендикулярную к ней прямую b:
-Проведём окружность произвольного радиуса с центром в произвольной точке (в нашем случае ,в точке О) так,что она пересечёт прямую a в точках M и N;
-Проведём две окружности радиуса MN с центрами в точках M и N так,что они пересекутся в двух точках F и S;
-Проведём прямую b через точки F и S; точки F,O,S лежат на одной прямой b;
-a⊥b.
3)Проведём окружность произвольного радиуса с центром в точке О так,что она пересечёт прямые a и b в двух точках каждую;нам нужны лишь две : A и B (A∈a,B∈b)
4)Соединим точки A и B.
5) AOB -- прямоугольный равнобедренный треугольник.
Прямой угол можно построить и с циркуля!
Поворот вокруг вершины B на 90 градусов:
1) Транспортиром откладываваем два прямых угла: один от точки B для от прямой a,другой от этой же точки,но для прямой AB --
прямые a и c образуют угол в 90°,AB и d так же.
2) Раствором циркуля берём расстояние BO и переносим его на прямую c,откладывая от точки B;отмечаем точку O'. Затем берём расстояние AB и откладываем на прямой d от точки B его же,отметив точку A'. AB=A'B,OB=O'B. Соединим точки: B с O',O' с A',A' с B
3) A'O'B -- образ треугольника AOB при повороте на 90 градусов по часовой стрелке вокруг точки B.