Объяснение:
1. На любой прямой можно взять сколько угодно точек, принадлежащих этой прямой и не принадлежащих этой прямой.
Другая прямая, хоть параллельная, хоть перпендикулярная, ни при чём.
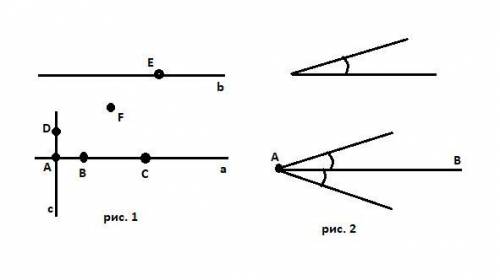
Смотрите рис. 1.
Точки A, B, C принадлежат прямой а.
Точки D, E, F не принадлежат прямой а.
Точка Е принадлежит параллельной прямой b.
Точка D принадлежит перпендикулярной прямой c.
Точка А принадлежит и прямой а и прямой с.
2. Два угла можно построить на одном луче, с двух разных сторон.
Смотрите рисунок 2.
Угол образец сверху. Снизу два угла, равных образцу, у луча AB.
Доказать равенство отрезков по представленному рисунку.
Доказательство:
Докажем, что AO = OC, исходя из признаков равенства треугольников.
1) Рассмотрим треугольники BCD и BAD.
BC = BA по условию (отмечено на рисунке);
CD = AD по условию (отмечено на рисунке);
BD - общая сторона.
Третий признак равенства: если три стороны одного треугольника соответственно равны трем сторонам другого треугольника, то такие треугольники равны.
ΔBCD = ΔBAD по третьему признаку (по трем сторонам).
2) В равных треугольниках соответствующие углы равны, соответствующие стороны равны.
Следовательно ∠CBD = ∠ABD, а значит ∠CBO = ∠ABO.
3) Рассмотрим треугольники CBO и BAO.
BC = BA по условию;
BO общая сторона;
∠CBO = ∠ABO из равенства треугольников BCD и BAD (см п.2).
Первый признак равенства треугольников: если две стороны и угол между ними одного треугольника соответственно равны двум сторонам и углу между ними другого треугольника, то такие треугольники равны.
ΔCBO = ΔBAO по первому признаку (по двум сторонам и углу между ними).
4) Так как в равных треугольниках соответствующие стороны равны, то АО=ОС.
Доказано.
Решение
Пусть ABCDA1B1C1D1 – данная призма, основания ABCD и A1B1C1D1 которой – ромбы со стороной 2, причём DAB = 30o и AA1 = BB1 = CC1 = DD1 = 1 . Если DF – высота ромба ABCD , опущенная на сторону AB , то по теореме о трёх перпендикулярах D1F AB , поэтому DFD1 – линейный угол двугранного угла между плоскостями основания ABCD и диагонального сечения AD1C1B . Так как DF = AD sin 30o = 1 , то tg DFD1 = = 1 . Поэтому DFD1 = 45o < 60o . Значит, данная в условии секущая плоскость пересекает рёбра A1D1 и B1C1 . Обозначим через M и N соответствующие точки пересечения. Поскольку плоскости оснований параллелепипеда параллельны, а также параллельны плоскости противоположных боковых граней, то четырёхугольник AMNB – параллелограмм. Пусть MP – перпендикуляр, опущенный из точки M на плоскость основания ABCD . Поскольку плоскости AA1D1D и ABCD перпендикулярны, точка P лежит на их прямой пересечения AD . Если MQ – высота параллелограмма AMNB , опущенная на сторону AB , то по теореме о трёх перпендикулярах PQ AB , поэтому MQP – линейный угол двугранного угла между плоскостями AMNB и ABCD . По условию задачи MQP = 60o . Значит,
MQ = = = .
Следовательно,
SAMNB = AB· MQ = 2· = .
Объяснение: