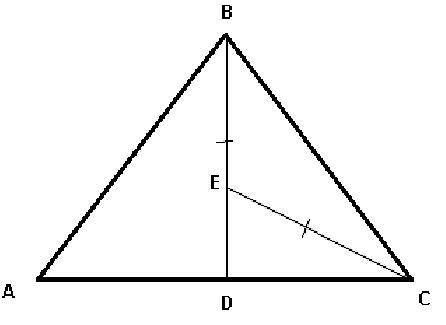
Пусть точка Е лежит на медиане BD равнобедренного треугольника
ED = 14 см и CE = 50 см. Поскольку отрезки от концов боковой
стороны равноудалены, то BE = CE = 50 см. Из прямоугольного
треугольника EDC по теореме Пифагора:
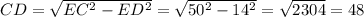 см
см
Поскольку BD - медиана равнобедренного треугольника, то
она является и высотой и биссектрисой. Тогда BD = 14+50 = 64 см.
По теореме Пифагора из прямоугольного треугольника BDC:
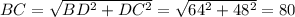 см.
см.
AC = 2 * DC = 2 * 48 = 96 см. Тогда периметр треугольника равен
P = AB + BC + AC = 80 + 80 + 96 = 256 см
S =S(ABCD) -?
S =( (a+b)/2) ) *h =((a+3) /2) *2r =(a+3)*r .
(Из ΔAOB : OT ⊥ AB , OT =r ,где O центр вписанной окружности ) .
∠AOB =180° -(∠A/2+∠B/2) =180° -(∠A+∠B)/2 =180° -180°/2 =90°.
r =√( (a/2)*(b/2) ) =(1/2) √(ab) ;
3 =(1/2) √(a*3) ;
9 =(a/2)*(3/2) ⇒a =12 .
S =(12+3)*3 =45.
* * * или иначе :
(AB +CD) =(AD +BC) свойство описанного четырехугольника
2AB =(a+b)⇒AB =(a+b)/2 .
Проведем BH ⊥ AD . AH =(a-b)/2 .
Из ΔABH :
BH² =AB² -AH² =((a+b)/2)² -((a-b)/2) =ab ;
(2r)² =√(ab) ;
r =(1/2)*√(ab) . и т.д.
Удачи !