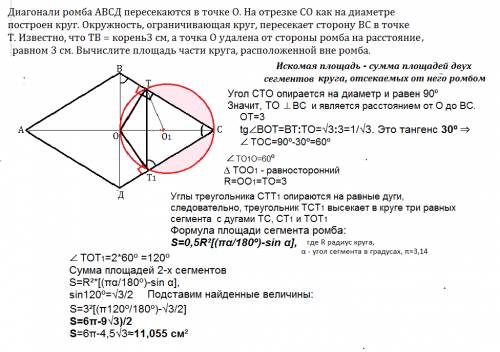
Искомая площадь - сумма площадей двух сегментов круга, отсекаемых от него ромбом.
Угол СТО опирается на диаметр и равен 90º
Расстояние от точки до прямой - длина отрезка из этой точки, перпендикулярного к этой прямой.
ОТ ⊥ ВС и является расстоянием от О до ВС.
ТО=3 см ( расстояние от точки до прямой - перпендикуляр)
Формула площади сегмента ромба:
S=0,5R²[(πα/180º)-sin α],
где R радиус круга, α - угол сегмента в градусах, π≈3,14
∆ ВОС~∆ ВОТ ( прямоугольные с общим углом при В)
∠ВОТ=∠ВСО
tg∠ВОТ=ВТ:ТО=√3:3=1/√3. Это тангенс 30º
∆ ТО1С равнобедренный.
∠ ТСО₁=∠ СТО₁
∠ ТО₁С=180-2∠ТСО₁
Отсюда ∠ТО₁С=180º-2*30º=120º
Из ∆ ТОС
ОС=ТО:sin30º=3:0,5=6 см
R=ОС:2=3 см
Сумма площадей 2-х сегментов
S=R²[(πα/180º)-sin α],
sin 120º=√3/2
Подставим найденные величины:
S=3²[(π120º/180º)-√3/2]
S=6π-9√3)/2
S=6π-4,5√3≈11,055 см²
-------
В приложении решение дано несколько иное, хотя принцип тот же.
Половина диагонали d/2 = (а/2)*√2 ≈ 16,97056.
a) Боковое ребро L = √(Н² + (d/2)²) ≈ 18,76166.
Апофема А = √(H² + (a/2)²) ≈ 14,42221.
Периметр Р = 4a = 96.
Площадь основания So = a² = 576.
б) Площадь боковой поверхности Sбок = (1/2)РА ≈ 692,2658.
Площадь полной поверхности S = So + Sбок ≈ 1268,266.
Объём V = (1/3)SoH =1536
Уг.бок.грани α = 0,588003 радиан = 33,69007°.
Угол бок.реб β = 0,440511 радиан = 25,2394°.
Выс.к бок.реб hб = 18,44895.
Уг.межбок.гр γ = 2,335479 радиан = 133,8131°.