∠А (∠ВАК) = 96°
∠К (∠АКМ) = 73°
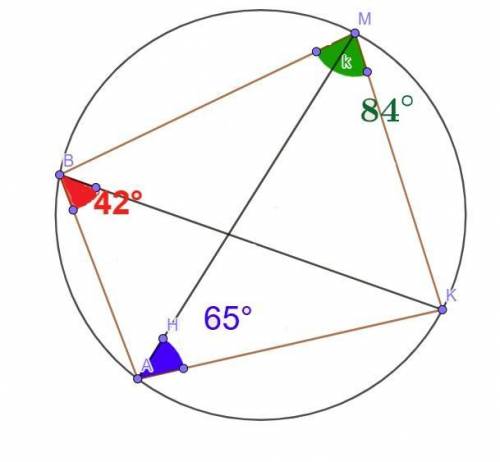
∠М (∠ВМК) = 84°
∠В (∠АВМ) = 107°
Объяснение:
Сума протилежних кутів вписаного у коло чотирикутника дорівнює 180 градусам (властивість).
∠ВМК+∠ВАК = 180°
∠ВАК = 180° - ∠ВМК = 180° - 84° = 96°
∠АВК та ∠АМК - вписані кути. Вони спираються на дугу АК.
Вписані кути, що спираються на одну дугу, рівні. ⇒
∠АМК = ∠АВК= 42°
Так як сума кутів трикутника дорівнює 180°, то з ΔАМК знаходимо кут ∠АКМ:
∠КАМ+∠АМК+∠АКМ = 180°
∠АКМ = 180°- ∠КАМ-∠АМК= 180°-65°-42°= 73°
Так як Сума протилежних кутів вписаного у коло чотирикутника дорівнює 180 градусам, маємо:
∠АВМ + ∠АКМ = 180°
∠АВМ = 180° - ∠АКМ = 180°- 73° = 107°
R = V3/3 * a, где R - радиус описанной окружности, V - знак корня, а - сторона равностороннего треугольника
Но, если хочешь, можно и посчитать. Только чертеж сделай и смотри внимательно.
Дело в том, что в равностороннем треугольнике и высоты, и биссектрисы, и медианы пересекаются в одной точке. И эта точка является центром окружности, описанной около этого треугольника.
Проведи медиану (высоту, биссектрису) из любого угла. Т. е. раздели треугольник пополам. Получился прямоугольный треугольник (высоту ведь опустили) , у которого гипотенуза равна 6 см, а катет равен 3 см (половина, медиана ведь)
По теореме Пифагора находим второй катет . Получим 3V3 (три корня из трех)
А медианы в точке пересечения делятся на отрезки в отношении 2:1. Значит, та часть, которая является радиусом окружности -- это 2V3, а другая часть 1V3
а если бы подставила в формулу, получила бы такой же ответ R= V3/3 *6= 2V3