Пусть AC=x, тогда в ΔABC по формуле Герона:
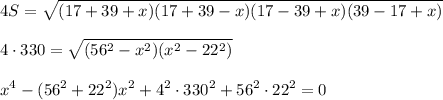
Решим квадратное уравнение относительно x².
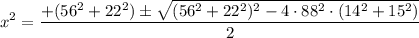
Далее немного вычислений, и зная, что x>0, как сторона треугольника, получим:
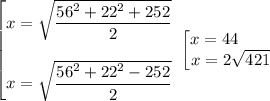
Пусть KL=a, KN=b.
Рассмотрим случай, когда AC=44.
В ΔABC по теореме косинусов:
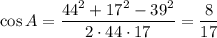
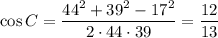
По формуле связи косинуса и тангенса:
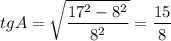
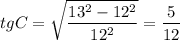
В прямоугольных треугольниках AKL и CNM выразим AK и CN через a, основываясь на определении тангенса острого угла в прямоугольном треугольнике.
AK=8a/15; CN=12a/5
AC=AK+KN+NC=(44a/15)+b=44
P(KLMN)=2a+2b=59
Составим систему и определим S(KLMN)=ab
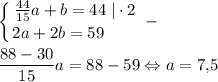
b=(59-15)/2=22
ab=7,5·22=165
Теперь всё тоже самое только AC=2√421.
В ΔABC по теореме косинусов:
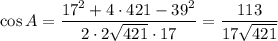
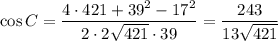
По формуле связи косинуса и тангенса:
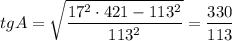
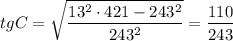
AK=113a/330; CN=243a/110
AC=AK+KN+NC=(421a/330)+b=2√421
P(KLMN)=2a+2b=59
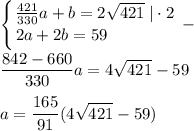
Заметим, что проекция AB на AC равна AB·cosA=113/√421
Получается, что AK=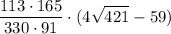
> 113/√421.
Таким образом при АС=2√421 картинка другая, которая не удовлетворяет условию задачи.
ответ: 165.
Объяснение:
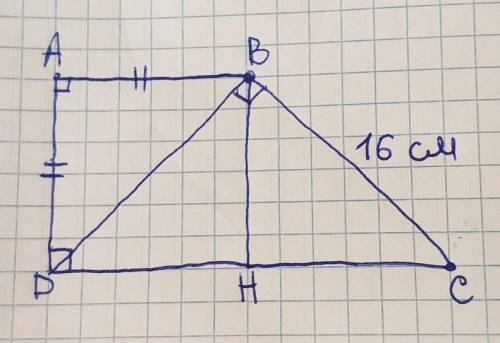
Дано:
Угол BAD= угол ADH=90°
BC=16см
АВ=АD
Рассмотрим прямоугольный ∆АВD.
Так как по условию меньшее основание трапеции равно меньшей боковой стороне, тоесть AD=AB, то ∆ADB равнобедренный с основанием BD, следовательно:
угол ADB= углу АВD.
Найдем угол ADB:
В прямоугольном треугольнике сумма острых углов равна 90°, тогда угол ADB=90°:2=45°
Рассмотрим ∆BDC.
Угол DBC=90° (так как по условию диагональ проведённая из тупого угла перпендикулярна большей боковой стороне), следовательно ∆BDC прямоугольный
Угол BDC=угол ADH– угол ADB=90°–45°=45°
Сумма острых углов в прямоугольной треугольнике равна 90°, следовательно угол BCD=90–угол BDC=90°–45°=45°
Получим: угол ВСD = угол BDC, тогда ∆BDC равнобедренный с основанием DC, следовательно BC=BD.
Так как ВС по условию 16 см, то и ВD=16 см.
Проведём высоту BH из угла АВС к стороне DC.
Так как по условию АВ=AD, а угол DAB=90° (прямой угол трапеции), то ABHD — квадрат.
Следовательно: AD=BH=DH
Найдем АD.
По теореме Пифагора BD²=AD²+AB²
16²=2AD²
256=2AD²
128=AD
AD=√128
AD=8√2
Sтрапеции=Sкв+Sтреугольника BHC
Sкв=а²
Где а сторона квадрата
Sкв=(8√2)²=128 см²
Треугольник BHC прямоугольный с прямым углом BHC ( так как BH высота)
Так как угол BCH=45°, то угол HBC=90°–угол BCH=90°–45°=45°
Тогда прямоугольный треугольник BHC равнобедренный.
Площадь прямоугольного равнобедренного треугольника равна половине квадрата стороны, тоесть:
S=0,5*a²
Подставим значения:
S=0,5*(8√2)²=64 см²
Найдем общую площадь:
S=128+64=192 см²
Ртрапеции=AB+AD+DH+HC+BC=8√2+8√2+8√2+8√2+16=4*(8√2)+16=32√2+16 (см)
ответ: S=192 см²
Р=32√2+16 см
использованы формулы: площадь полной поверхности, площадь ромба, теорема Пифагора
Площадь полной поверхности параллелепипеда равна 2 площади основания + площадь боковой поверхности. Т. к. большая диагональ парал-да образует с боковым ребром угол 45 град., то большая диагональ ромба равна боковому ребру - получается прямоугольный треугольник с острым углом 45 град. след. он равнобедренный. Находим по теореме Пифагора. Пусть ребро - х, тогда х2 + х2 = (16 корней из 2) 2, 2 х х2=16 х 2, х2=256, х=16. Вторая диагональ ромба и боковое ребро равны 16 см. Площадь ромба ноходим, как половину произведения его диагоналей, а площадь боковой поверхности - периметр основания на боковое ребро. Сторона основания (по т. Пифогора) равна корню кв. из 6 в квадрате + 8 в квадрате (диагонали ромба перпендикулярны и делятся точкой пересечения пополам) 36+64=100, т. е. 10.
S=2Sосн.+Sбок.=2 х 1/2 х 12 х16 + 10 х 4 х 16 = 16 (12+40) = 832 кв. см.