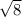ответ:
1. К
2. IV
3. 7 или -5
4. (0;0,5)
5. 2√73
6. (3√3; 1) или (-3√3; 1)
7. ромб
Объяснение:
1. Координаты точки К (3;0)
2. Координаты x>0, y<0 могут быть только в IV четверти
3. АВ=10=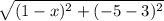 
Приводим к квадратному уравнению 
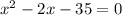. Решаем через дискриминант и получаем х1=7, х2=(-5)
4. Координаты этой точки, допустим М (0;у) Нужно найти у. Поскольку эта точка М равноудалена от точек Д и Е, то расстояние между ними одинаковое, то есть по формуле расстояния между точками находим расстояния между ДМ и ЕМ и приравниваем. Решаем уравнение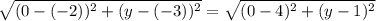 
и получаем у=0,5
5. Координаты точек А(х;0), В(0;у) В формулу середины отрезка подставляем эти координаты и координаты точки М(-3;8): (-3)=(х+0)/2 х=(-6); 8=(0+у)/2 у=16. Теперь по формуле расстояния между точками находим расстояние между точками АВ и получаем АВ=2√73
6. Вершина В может быть или в 1й четверти, или во 2й четверти. По формуле расстояния между точками находим расстояние между точками А и С. Получаем 6. Поскольку ABC равносторонний треугольник, то АС=АВ=ВС=6. По формуле расстояния между точками находим расстояния между АВ и ВС и приравниваем. Решаем уравнение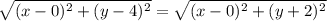 
и получаем у=1.
Подставляем значение у=1 в любую из сторон уравнения и получаем х1= 3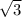
, х2= -3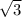
7. Если высчитать расстояние между точками, то есть стороны четырехугольника, то они равны: АВ=ВС=СД=АД=2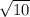
. То есть это либо ромб, либо квадрат. Дальше высчитываем длину диагоналей тоже как расстояние между точками: АС=2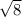, ВД=4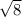. То есть диагонали не равны, значит это не квадрат, а ромб.
Высота правильной четырёхугольной пирамиды равна 12 см, а сторона основания равна 24 см. Вычисли двугранный угол при основании.
——————————————————
Основание правильной четырехугольной пирамиды – квадрат.
Все боковые грани правильной пирамиды образуют с плоскостью основания равные углы, а высота проходит через центр основания, который является центром вписанной и описанной около основания окружностей.
Двугранный угол здесь образован радиусом вписанной окружности и апофемой, как отрезками. перпендикулярными ребру основания в одной точке (по т. о трех перпендикулярах).
Радиус вписанной в квадрат окружности равен половине его стороны.
r=24:2=12 (см)
Соединив основание апофемы с центром основания ( основанием высоты пирамиды), получим прямоугольный треугольник.
При этом катеты- высота пирамиды и половина стороны основания - равны 12 см.
Следовательно, треугольник - равнобедренный. Острые углы равнобедренного прямоугольного треугольника равны 45º.⇒ Искомый угол равен 45º.
пусть угол А=х, тогда в=4х, с=4х-90
х+4х+4х-90=180(сумма углов треугольника)
х=30 угол А
В=120
С=30
Этот тр-ник равнобедренный, следовательно АВ=Вс