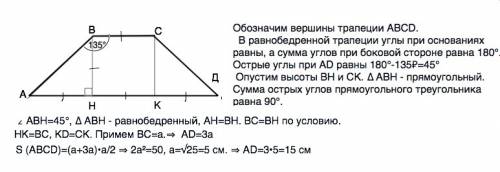
Обозначим вершины трапеции АВСD. В равнобедренной трапеции углы при основаниях равны, а сумма углов при боковой стороне равна 180°.
Острые углы при АD равны 180°-135₽=45°
Опустим высоты ВН и СК. ∆ АВН - прямоугольный. Сумма острых углов прямоугольного треугольника равна 90°.
∠ АВН=45°, ∆ АВН - равнобедренный, АН=ВН. ВС=ВН по условию. НК=ВС, КD=СК. Примем ВС=а.⇒ АD=3а
S (АВСD)=(а+3а)•a/2 ⇒ 2a²=50, a=√25=5 см. ⇒ АD=3•5=15 см

ответ: 20см
Объяснение:
чертеж: окружность, провести диаметр ДС, хорда ВА _|_ ДС,
ВА пересечет ДС в т.К , ДК=5, КС=20. Xорда, перпендикулярная
диаметру,делится точкой К пополам, ВК =АК, Тр-ки ДВС и ДАС-
прямоугольные, т. к. вписанные углы А и В опираются на диаметр ДС,
тр-к ДВС по свойству пропорциональных отрезков BK^2=DK*DC,
BK^2=5*20=100, BK=10, BA=2*10=20(см)