1. уравнение прямой: y=kx+b
подставим координаты в уравнение: -3=2k+b и 1=4k+b
из второго уравнения: b=1-4k
теперь подставим b в первое уравнение: -3=2k+1-4k => -3-1=2k-4k => -4=-2k =>k=2
теперь подставим k во второе уравнение: 1=4*2+b
b=1-8
b=-7
следовательно уравнение принимает вид: y=2x-7
2. теперь подставим y=0 . получается 0=2*х-7
2х=7
х=3,5 значит (3,5; 0)
Подробнее - на -
АС=10 ВС=11 АВ=17
Объяснение:
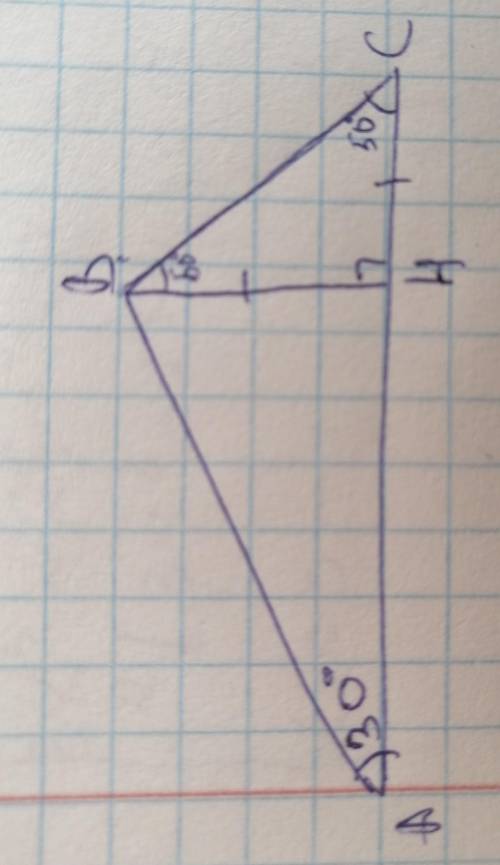
ВНперпендикулярен АС
ТреугольникВНС- равнобедр, т.к. уголС=углуНВС=50°
ВН=НС
пумть:
ВН=х
АС=10
АН=10-х
tg30°=BH/AH=x/10-x
x(10+tg30°)=tg30°
x=tg30°/10+tg30°=1/корень3/10+1/корень3=1/10+корень3
ВН=1/10+корень3=СН
sin50°=BH/BC(0.8рад)
BC=BH/sin50°=1/10+корень3 : 8/10=5/40+4корень3(примерно 0,11)
ВС=11
sin 30°=BH/AB
AB=BH/sin30°=1/10+корень3 : 1/2= 2/10+корень3(примерно 0,17)
АВ=17
наименьшая сторона АС
(чертёж на быструю руку)
На счёт этой задачи не уверена правильный ли ответ. Было бы лучше есть место 50° было 45°.
Объяснение:
1. Строим перпендикуляр. Один из углов треугольника- 30 градусов, следовательно противолежащий, нужный нам, катет равен половине гипотенузы или 2 см
2. Строим перпендикуляр. На рисунке изображен треугольник с двумя равными углами, следовательно, он равнобедренный, следовательно высота, которую мы провели, является также медианой. То есть расстояние от середины основания треугольника до точки С- 7см. По сумме острых углов прямоугольного треугольника находим второй острый угол и видим, что он равен первому. То есть треугольник равнобедренный и длина искомого перпендикуляра также равна 7 см.
3. Строим перпендикуляр. Получившийся катет лежит напротив угла в 30 градусов и, следовательно, равен половине гипотенузы или m\2.
4. Большой треугольник равнобедренный, следовательно, его углы при основании равны. То есть угол NKA равен 30 градусов.(180-60=120. 120\2=60. 60\2=30.Опустим перпендикуляр из точки А на прямую а. Получили прямоугольный треугольник с углом в 30 градусов. То есть длина искомого перпендикуляра равна половине длины отрезка КА и равна 3,5 см.