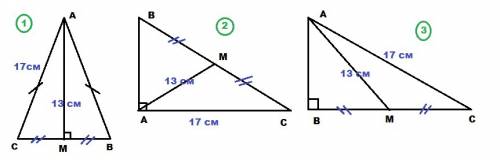
Задача с неполным условием, имеет бесконечно много решений в зависимости от формы треугольника. Рассмотрим три возможных варианта.
1) ΔABC - равнобедренный, AC = AB; AM=13 см; AC = 17 см
AM - медиана, в равнобедренном треугольнике одновременно высота ⇒
CM = MB; AM ⊥ CB
ΔAMC - прямоугольный, ∠AMC=90°; AM=13 см; AC = 17 см
Теорема Пифагора :
CM² = AC² - AM² = 17² - 13² = 120 = (2√30)²
CM = 2√30 см
BC = 2 CM = 2*2√30 = 4√30 см
BC = 4√30 см
=========================================
2) ΔABC - прямоугольный; ∠BAC = 90°; AM=13 см; AC = 17 см
AM - медиана в прямоугольном треугольнике, проведенная к гипотенузе, равна половине гипотенузы.
BC = 2 AM = 2*13 = 26 см;
BC = 26 см
====================================
3) ΔABC - прямоугольный, ∠ABC = 90°; AM=13 см; AC = 17 см
AM - медиана ⇒ BM = MC; BC = 2BM
Теорема Пифагора
AB² = AC² - BC² = 17² - (2BM)² = 289 - 4BM²
Теорема Пифагора для ΔABM
AB² = AM² - BM² = 13² - BM² = 169 - BM²
169 - BM² = 280 - 4BM²
3BM² = 111; BM² = 37
BM = √37 см ⇒ BC = 2BM = 2√37 см
BC = 2√37 см
Найти расстояние H от точки S до плоскости трапеции АВСД.
Пусть проекция точки S на плоскость АВСД - точка О.
Длину стороны АВ примем равной х.
Точка О тоже равноудалена от сторон трапеции и, поэтому, находится на пересечении биссектрис прямых углов А и В.
Поэтому перпендикуляр ОЕ из точки О на АВ делит АВ пополам,
Тогда ВЕ = ОЕ = (х/2).
Продлим стороны АВ и СД до пересечения в точке К.
Отрезок КО - биссектриса угла АКД (пусть это угол α).
Отрезок КВ по подобию равен 2х
Тангенс угла ОКЕ = α/2 равен ОЕ/КЕ = (х/2)/(2х + 0,5х) = х/(5х) = 1/5.
Тангенс полного угла α равен:
tg α = 2tg(α/2)/(1-tg²(α/2)) = (2/5)/(1-(1/25)) = (2*25)/(5*24) = 5/12.
Теперь можно определить высоту трапеции, равную стороне АВ.
АВ = (15 - 10)/tg α = 5/(5/12) = 12 см.
Отрезок ОЕ = х/2 = 12/2 = 6 см.
Находим искомое расстояние Н от точки S до плоскости трапеции.
Н = √(10² - ОЕ²) = √(100 - 36) =√ 64 = 8 см.