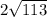Рисунок во вложении.
Назовем хорду АВ. Через точку В проведем касательную, из точки А проведем перепндикуляр АС к касательной-это и будет расстоянием от А до касательной. Получили прямоугольный треугольник АВС.
Теперь проведем диаметр окружности перпедикулярно хорде АВ. Он будет делить эту хорду пополам. Диаметр, перпендикулярный к хорде, делит эту хорду и стягиваемые ею дуги пополам. Точку пересечения хорды и диаметра назовем К .
Проведем радиус ОВ. Так как ОВ перпендикулярен касательной и АС перпендикулярен касательной, то ОВ//АС. Углы 1 и 2 накрест лежащие, значит они равны.
Рассмотрим треугольники АВС и ВОК: они прямоугольные и имеют по равному острому углу, значит они подобны. Из подобия следует, что ОВ:АВ=АС:ВК => ОВ:12=6:8 => ОВ=9
ответ: 9см.
Расстояния от середины гипотенузы до катетов это перпендикуляры опущенные на катеты из середины гипотенузы
Рассмотрим треугольник АМК (прямоугольный) и треугольник NKB (прямоугольный):
Они равны по стороне и двум прилежащим к ним углам.
Угол NBK = углу ANM как соответствующие при пересечении двум параллельных прямых СВ и MN третьей прямой АВ.
Угол MAN = углу KNB как соответствующие при пересечении двум параллельных прямых AC и NK третьей прямой АВ.
AN = NB из условия (АВ -гипотенуза).
Следовательно, треугольник АМК (прямоугольный) и треугольник NKB (прямоугольный) равны по второму признаку, то есть по стороне и двум прилежазщим к ней углам.
Следовательно, все стороны треугольника АМК соответственно равны сторонам треугольника NKВ. А, следовательно, АМ = NK = 8, MN = KB = 7.
Тогда АС = АМ + МС = 8+8=16.
ВС = СК + КВ = 7+7=14.
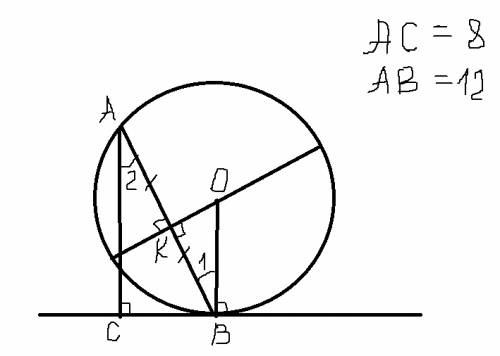
Дальше найдем АВ по теореме пифагора, т. к. треугольник АСВ прямоугольный:
ответ: 14, 16,