угол КВО=45°
Объяснение:
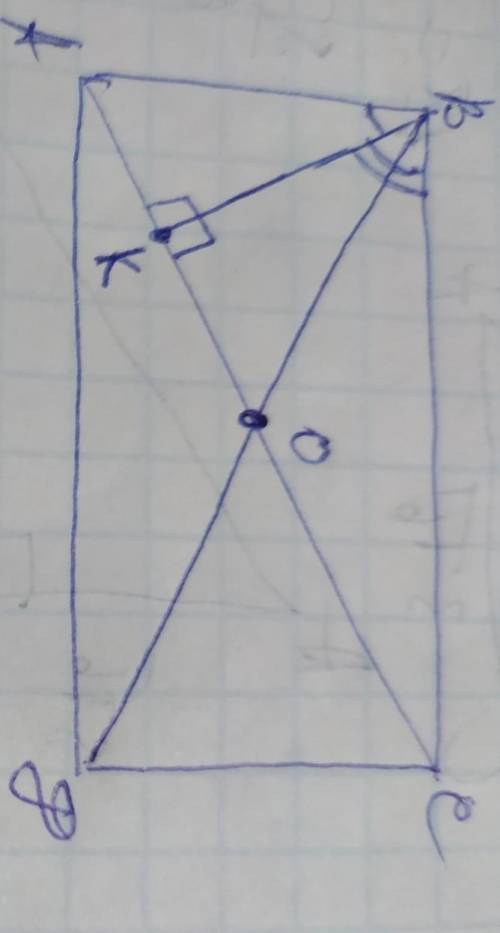
обозначим вершины прямоугольника ABCD с диагоналями АС и ВД, точку их пересечения О, а перпендикуляр ВК, пропорции углов обозначим х и 3х и, так как сумма этих двух углов составляет 90°, составим уравнение:
х+3х=90
4х=90
х=90÷4
х=22,5.
Итак: угол АВК=22,5°, тогда угол КВС=22,5×3=67,5°.
Рассмотрим полученный ∆АВК. Он прямоугольный, угол АВК=22,5°, а так как сумма острых углов прямоугольного треугольника составляет 90°, то угол ВАК=90-22,5=67,5°.
Рассмотрим ∆АВО. Он равнобедренный, поскольку диагонали прямоугольника пересекаясь делятся пополам, поэтому АО=ВО, а АВ- его основание и углы при основании равны:
уголВАО=углу АВО=67,5°. Угол ВАО в ∆АВО и угол ВАК в ∆АВК является общим и равен 67,5°. Тогда угол КВО=67,5-22,5=45°
AD = 4 см.
BK = 3 см.
AC = 8 см.
△ADC и BKC - прямоугольные.
Найти:ВС - ?
Решение:Рассмотрим △ADC:
Если в прямоугольном треугольнике катет равен половине гипотенузы, то напротив лежащий угол равен 30°.
АС = 2AD => ∠C = 30˚
Рассмотрим △ВКС:
Если острый угол прямоугольного треугольника равен 30°, то напротив лежащий катет равен половине гипотенузы.
BK - напротив лежащий катет => BC = 3 * 2 = 6 см.
ответ: 6 см.