Дано :
параллелограмм NPKA
<ANK = 45°
<KNP = 65°
Найти:
<А, <К, <Р, <N, <NKA, <NKP = ?
<N = <ANK + <KNP = 45° + 65° = 110°
<N = <K = 110° (св-во параллелограмма - противоположные углы равны)
<А = 180° - <К = 180° - 110° = 70° (свойство параллелограмма - углы, прилежащие к любой стороне, в сумме равны 180°)
<Р = <А = 70° (св-во параллелограмма - противоположные углы равны)
<NKA = <KNP = 65° (н.л. при NP//AK и секущей NK)
<NKP = <K - <NKA = 110° - 65° = 45°
ответ: <А = <Р = 70° ; <К = <N = 110° ; <NKA = 65° ; <NKP = 45°
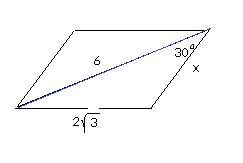


Відповідь:
1) гострий кут =180-90-60=30*
Гіпотенуза= в два рази більше катета що лежить проти кута 30* тому гіпотенуза= 2•12=24см
2)кутА=180-120=60*(суміжні кути в сумі дають180*)
КутС=180-90-60=30*
Гіпотенузи = в два рази більше катета що лежить проти кута 30* тому гіпотенуза=10см
3)DA=DB так як трикутник рівнобедрений то його бічні сторони рівні і ще до того кути при основі рівні тому DA=DB