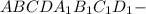 правильная четырехугольная призма
правильная четырехугольная призма
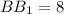 см
см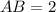 см
см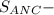 ?
?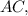 так как
так как 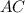 ⊂
⊂ 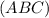 и
и 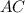 ⊂
⊂ 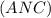
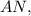 так как
так как 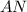 ⊂
⊂ 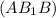 и
и 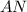 ⊂
⊂ 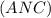
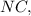 так как
так как  ⊂
⊂ 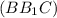 и
и  ⊂
⊂ 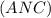
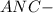 искомое сечение
искомое сечение 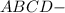 квадрат
квадрат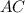 ∩
∩ 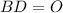
 см
см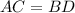 ( как диагонали квадрата)
( как диагонали квадрата)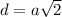
 см
см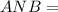 Δ
Δ 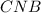 ( по двум катетам) ⇒
( по двум катетам) ⇒ 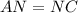
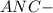 равнобедренный
равнобедренный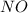 ⊥
⊥ 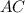
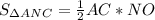
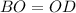
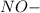 средняя линия Δ
средняя линия Δ 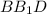
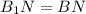 (по условию)
(по условию) 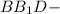 прямоугольный
прямоугольный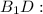
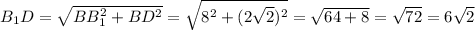 см
см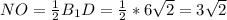 см
см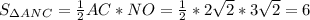 cм²
cм²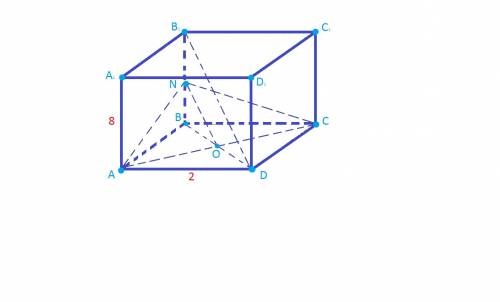
Так как BD перпенд. плоскости, то BD перпенд.AD и BD перпенд. DC, по определению синуса имеем
sin 45=BD/BC, BС=6sqrt(2)
sin 60=BD/AB, AB=4sqrt(3)
треуг.АВС прымоуг. по условию, АС^2=36*2+16*3=72+48=120, AC=sqrt(120)=2sqrt(30)