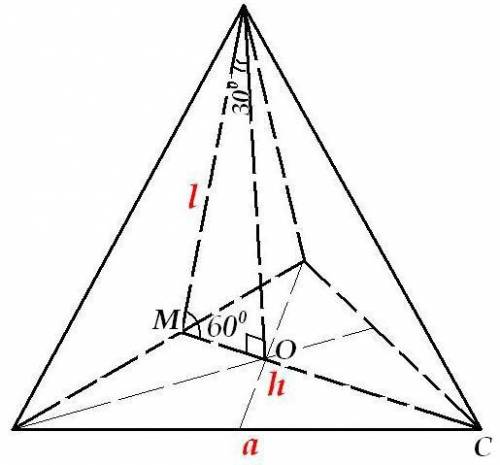
-сторона основания,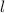 
- апофема, 
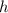- высота основания. Эти три величины потребуются для всего вычисления.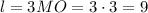
:
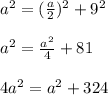
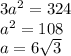
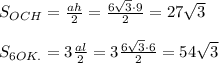
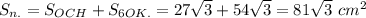
Построение сводится к проведению перпендикуляра из точки к прямой.
Из вершины А, как из центра, раствором циркуля, равным АС, делаем насечку на стороне ВС. Обозначим эту точку К.
∆ КАС- равнобедренный с равными сторонами АК=АС.
Разделив КС пополам, получим точку М, в которой медиана ∆ КАС пересекается с основанием КС. Т.к. в равнобедренном треугольнике медиана=биссектриса=высота, отрезок АМ будет искомой высотой.
Для этого из точек К и С, как из центра, одним и тем же раствором циркуля ( больше половины КС) проведем две полуокружности. Соединим точки их пересечения с А.
Отрезок АМ разделил КС пополам и является искомой высотой ∆ АВС из вершины угла А.
Сумма углов треугольника = 180°.
Если угол В = 110°, то сумма углов А и С = 70°. Угол ОАС - это половина от угла А, а угол ОСА - это половина от угла С. Соответственно, если углы А и С в сумме 70°, то их половины в сумме 35°.
Сумма углов любого треугольника = 180°, поэтому в треугольнике СОА угол АОС = 180°-35°=145°.