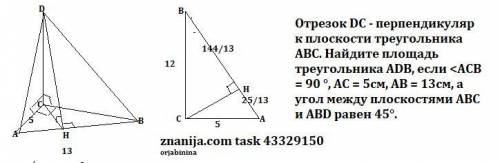
Отрезок DC - перпендикуляр к плоскости треугольника АВС. Найдите площадь треугольника АDB, если <АСВ = 90 °, АС = 5см, АВ = 13см, а угол между плоскостями АВС и АВD равен 45°.
Объяснение:
1) Т.к. угол между плоскостями АВС и АВD равен 45° , то построим линейный угол данного двугранного. Пусть DH ⊥AB, тогда по т. о трех перпендикулярах СН⊥АВ. Значит ∠СНD линейный угол данного двугранного ∠СНD =45°.
2)S(ABD)=1/2*АВ*DH .Найдем DH
3)ΔАВС-прямоугольный , по т. Пифагора СВ=√(13²-5²)=12 (см).
По метрическим соотношениям о среднем пропорциональном в прямоугольном треугольнике :
СВ²=АВ*НВ , 12²=13*НВ , НВ =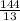 (см) .
(см) .
Тогда АН=АВ-НВ =13- 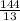 =
=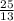 (см).
(см).
СН =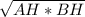 , CH=
, CH=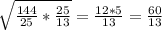 (см).
(см).
4)ΔCHD-прямоугольный , ∠CHD=45° . sin45°=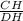 ,
, 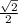 =
= 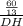 ,DH=
,DH=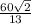 см.
см.
5) S(ABD)=1/2*13* 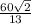 =30√2 (см²).
=30√2 (см²).
Внешний угол B треугольника равен 180° - ∠ B
Биссектриса ВК делит этот угол пополам ( отмечены на рис. синими дугами)
∠КВА = (180° - ∠B)/2= 90°- (∠B)/2
∠ КВС = ∠ КВА + ∠АВС= 90° - (∠B)/2 +∠ B= 90° + (∠ B)/2
Биссектриса КС делит угол С пополам.
∠ КСВ = ∠ (С/2)
Сумма углов треугольника КВС равна 180°
∠ ВКС = 180° - ∠КВС - ∠КСВ= 180° - 90° - (∠ B)/2 - (∠C/2)= 90° -(∠ B+∠C)/2=
= (180° - ∠ B - ∠C)/2 = (∠A)/2
Задача 2
Стороны параллелограмма относятся как 3:4,а его периметр равен 28 см.
Найдите стороны параллелограмма
Пусть одна сторона параллелограмма 3х, другая 4х, тогда периметр равен 3х+3х+4х+4х=14х
А по условию задачи 28
Составляем уравнение
14х=28
х=2
Одна сторона 3х= 3·2= 6 см , другая сторона 4х= 4·2= 8 см
ответ. 6 см и 8 см