Для даної задачі треба скористатися властивостями катетів та їх проекцій на гіпотенузу в прямокутному трикутнику.
Перший б
Катет прямокутного трикутника — середнє пропорційне між гіпотенузою 
і проекцією цього катета на гіпотенузу:
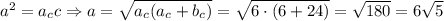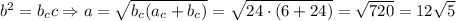см
см
Площа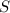 
прямокутного трикутника знаходится як півдобуток його катетів:
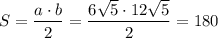см²
Другий б
Висота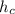 
прямокутного трикутника, що проведена до гіпотенузи з вершини прямого кута, — середнє пропорційне між проекціями катетів на гіпотенузу:
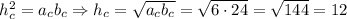см
Площа 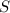будь-якого трикутника знаходиться як півдобуток його сторони на висоту, що проведена до цієї сторони. У нашому випадку — це півдобуток гіпотенузи і висоти 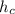, що до неї проведена:
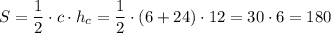см²
Відповідь: 180 см².
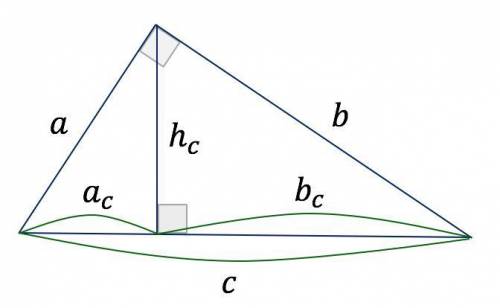
75 см²
Объяснение:
Прямоугольные треуг-ки ВНС и АН1С подобны по первому признаку подобия: два угла одного треуг-ка соответственно равны двум углам другого. В нашем случае углы АН1С и ВНС прямые, а угол С - общий. Для подобных треугольников можно записать отношение сходственных сторон:
ВН:АН1=10:12, k=5/6, СН:СН1=5:6, отсюда
CH1=6CH:5
В прямоугольном треуг-ке АН1С по теореме Пифагора находим АС:
АС²=AH1²+CH1²
Т.к. в равнобедренном треуг-ке АВС высота ВН, проведенная к основанию, является также и медианой, то СН=1/2АС, и выражение CH1=6CH:5 примет такой вид:
СН1=3АС:5.
Это значение для СH1 будем использовать в вычислении по теореме Пифагора:
АС²=12² + 9AC²/25
AC² - 9AC²/25=144
16AC²=3600
AC² = 225
AC=15 см
S ABC = 1/2AC*BH=7,5*10=75 см²