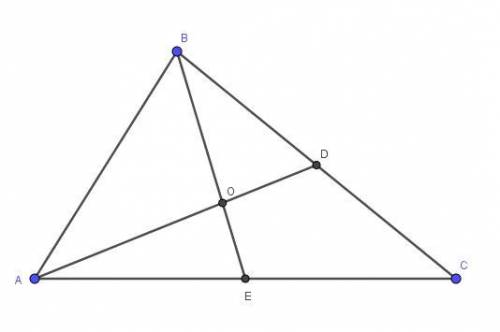
Медианы треугольника пересекаются в одной точке и делятся ею в отношении 2:1, считая от вершины треугольника.
Пусть 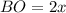 см и
см и 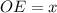 см, тогда
см, тогда 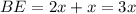 , что по условию он равен 9 см.
, что по условию он равен 9 см.
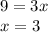
Следовательно, 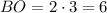 см и
см и 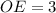 см
см
Аналогично, пусть теперь 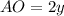 см и
см и 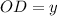 , тогда
, тогда 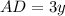 и по условию равен 12 см
и по условию равен 12 см
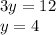
Таким образом, 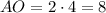 см и
см и 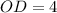 см.
см.
По условию медианы треугольника AD и BE взаимно перпендикулярны, следовательно
По теореме Пифагора из прямоугольного треугольника 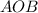
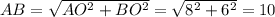 см
см
По теореме Пифагора из прямоугольного треугольника 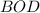
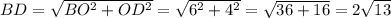 см
см
Тогда 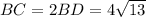 см
см
Из прямоугольного треугольника 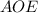 по теореме Пифагора
по теореме Пифагора
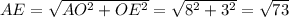 см
см
Тогда 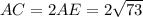 см
см
ответ: 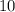 см;
см; 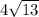 см;
см; 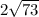 см.
см.
17; 9/17
Объяснение:
Диагональ параллелепипеда можно найти из обобщенной теоремы Пифагора: d^2 = a^2+b^2+c^2, где d диагональ пар-да, a,b,c - стороны пар-да. d^2 = 8^2+9^2+12^2 = 64+81+144=289. Значит DB1 = 17. Синус угла между диагональю DB1 и плоскостью AA1B можно найти из прямоугольного треугольника АВ1D1, гипотенуза DB1 = 17, противолежащий катет АD=9, поэтому sinB1 = 9/17