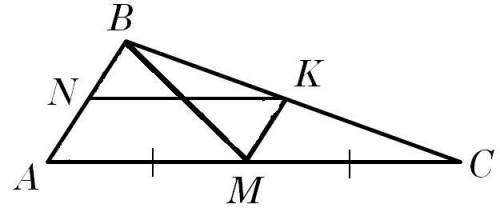
Объяснение: рисунок к задаче прилагаю.
Дано: ΔABC, т. M ∈ AC (AM = CM), т. K ∈ BC, т. N ∈ AB;
MK || AB, KN || AC, BK = 31 см, MC = 27 см, BN = 26 см.
Найти: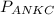 
.
Решение. Сразу найдем сторону AС. ВМ - медиана ⇒ AС = 2МС = 54 см.
Докажем, что NK - средняя линия треугольника АВС.
Поскольку MK || AB и KN || AC, то четырехугольник AMKN - параллелограмм. А это значит, что NK = AM = 1/2 AC = 27 см ⇒ NK - средняя линия треугольника по определению ⇒ BN = AN = 26 см, BK = KC = 31 см.
Ищем периметр: 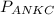= AN + NK + KC + AC = 26 + 27 + 31 + 54 = 138 см.
ОТВЕТ: 138.
Дано: ABCD - трапеция (AD || BC), K ∈ AD, BK || CD, AK = 1,2 м, KD = 0,75AK,
= 3,2 м
Найти: ср. линию;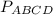
Решение. Пусть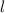
- средняя линия. Средняя линия трапеции равна полусумме оснований, т.е. 
.
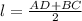В свою очередь, AD состоит из отрезков AK и KD. Тогда AD = AK + KD = AK + 0,75AK = 1,2 + 0,75 · 1,2 = 1,2 + 0,9 = 2,1 (см).
Поскольку BK || CD и AD || BC ⇒ KD || BC, то четырехугольник BKDC - параллелограмм ⇒ BC = DK = 0,9 (см).
Средняя линия: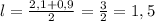
(см).
Т.к. BKDC - параллелограмм, то BK = CD.
Периметр: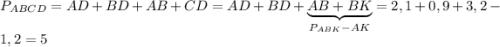
ОТВЕТ:
= 1,5 см, P = 5 см.