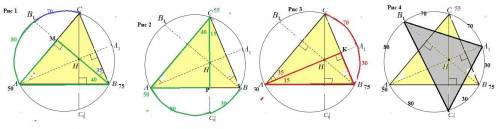
Ортоцентр H треугольника ABC отразили относительно сторон и получили точки A₁, B₁ и C₁. Найдите углы треугольника A′B′C′, если ∠A=50∘, ∠B=75∘.
Объяснение:
По свойству ортоцентра : "Точка, симметричная ортоцентру относительно стороны треугольника, лежит на описанной около него окружности". Значит все точки А, В, С,A₁, B₁ , C₁-лежат на окружности.
1)ΔАВМ -прямоугольный ,∠А=50°⇒ ∠АВМ=90°-50°=40° . Значит ∠МВС=75°-40°=35° .Поэтому дуги ∪ АВ₁=80° и ∪ В₁С=70° по т. о вписанном угле.
2)ΔАСР -прямоугольный ,∠А=50°⇒ ∠АСР=90°-50°=40° . Значит ∠РСВ=55°-40°=15° .Поэтому дуги ∪ АС₁=80° и ∪ С₁В=30° по т. о вписанном угле.
3)ΔАВК -прямоугольный ,∠В=75°⇒ ∠ВАК=90°-75°=15° . Значит ∠САК=50°-15°=35° .Поэтому дуги ∪ СА₁=70° и ∪ А₁В=30° по т. о вписанном угле.
)ΔА₁В₁С₁ , по т. о вписанном угле : ∠А₁=1/2*(80°+80)°=80° ,∠В₁=1/2*(30°+30)°=30° , ∠С₁=1/2*(70°+70)°=70°.
1) Пусть ΔАВС - прямоугольный, ∠С=90°, АВ - гипотенуза, АВ=12 см.
АС=х, ВС=х-2, Р(АВС)=26 см.
Составляем уравнение:
x+(x-2)+12=26;
2x-2+12=26;
2x+10=26;
2x=26-10;
2x=16;
x=8.
AC=8 см, ВС=8-2=6 (см).
Вообще, такого прямоугольного треугольника с катетами 6 см, 8 см, и гипотенузой 12 см не существует, так как не выполняется условие т.Пифагора:
6²+8²≠12²:
36+64≠144;
100≠144.
2.
1) Пусть ΔАВС - равнобедренный, АВ=ВС=2х, АС=х, Р(АВС)=15 см.
Составляем уравнение:
2х+2х+х=15;
5х=15;
х=3.
АС=3 см, АВ=ВС=2*3=6 см.
ответ: 6 см, 6 см.