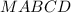 - правильная четырехугольная пирамида, около которой описан конус
- правильная четырехугольная пирамида, около которой описан конус 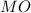 ⊥
⊥ 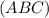
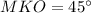
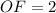 см
см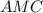 - осевое сечение конуса, где
- осевое сечение конуса, где 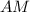 и
и 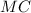 - образующие конуса
- образующие конуса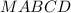 - правильная четырехугольная пирамида,
- правильная четырехугольная пирамида, 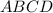
 ∩
∩ 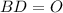
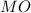 ⊥
⊥ 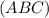
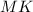 ⊥
⊥ 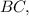 тогда
тогда 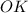 ⊥
⊥ 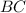 и
и 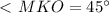 как линейный угол двугранного угла
как линейный угол двугранного угла 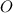 - центр окружности, описанной около квадрата
- центр окружности, описанной около квадрата 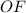 , т. е.
, т. е. 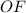 ⊥
⊥ 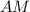
 тогда
тогда 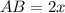
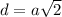 , где
, где 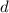 - диагональ квадрата,
- диагональ квадрата,  - сторона квадрата
- сторона квадрата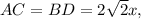 ( как диагонали квадрата)
( как диагонали квадрата)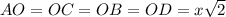
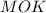 - прямоугольный, равнобедренный, следовательно
- прямоугольный, равнобедренный, следовательно 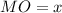
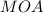 - прямоугольный
- прямоугольный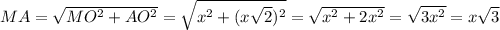
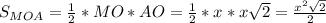 ,
,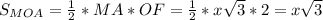
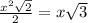
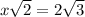
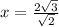
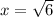
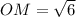 см
см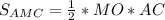
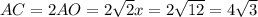 см
см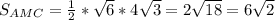 (см ²)
(см ²)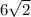 см²
см²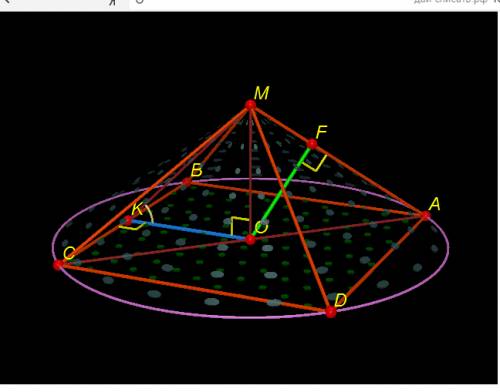
Пересечение этой окружности с прямой I и даст нам точки на прямой I, находящиеся на расстоянии "а" от точки М.
Проведем перпендикуляр МН из точки М к прямой I. Длина этого перпендикуляра - расстояние от точки М до прямой I.
Если значение "а" больше расстояния от М до I, то имеем две точки на прямой I, находящиеся на расстоянии "а" от точки М.
Если значение "а" равно расстоянию от М до I, то имеем одну точку на прямой I, находящуюся на расстоянии "а" от точки М.
Если значение "а" меньше расстояния от М до I, то точки на прямой I, находящейся на расстоянии "а" от точки М не существует.