1 Напишите теорему о сумме углов треугольника 2 Напишите формулировки некоторых свойств прямоугольных треугольников 3 В остроугольном треугольнике MNP биссектриса угла М пересекает высоту NК в точке О, причем ОК = 9 см. Найти расстояние от точки О до прямой MN. 4 Биссектриса прямого угла прямоугольного треугольника образует с гипотенузой углы, один из которых равен 70 градусов . Найти острые углы этого треугольника. 5 Один из углов прямоугольного треугольника равен 60 градусов , а сумма гипотенузы и меньшего катета равна 42 см. Найти длину гипотенузы.
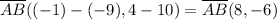 ;
; от точки A
от точки A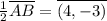 ;
; в обе возможные стороны
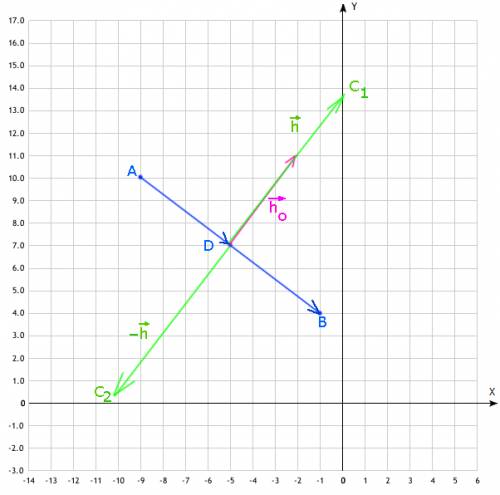
в обе возможные стороны перпендикулярен вектору основания
перпендикулярен вектору основания  , а значит его проекции накрест-пропорциональны с противоположным знаком:
, а значит его проекции накрест-пропорциональны с противоположным знаком: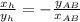 , что непосредственно следует из скалярного произведения, поскольку для перпендикулярных векторов должно выполняться:
, что непосредственно следует из скалярного произведения, поскольку для перпендикулярных векторов должно выполняться:  (II) ;
(II) ; пропорционален вектору
пропорционален вектору  , поскольку для вектора
, поскольку для вектора  выполняется и равенство (I) и равенство (II) осталось лишь найти масштаб вектора
выполняется и равенство (I) и равенство (II) осталось лишь найти масштаб вектора  ;
; имеет длину
имеет длину 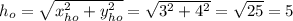 ;
;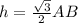 , т.к
, т.к 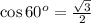 ;
;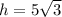 , а стало быть
, а стало быть  ;
;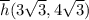 .
.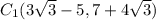 /// примечание:
/// примечание: 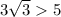 ;
;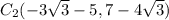 /// примечание:
/// примечание: 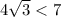 .
.
Построение сводится к проведению перпендикуляра из точки к прямой.
Из вершины А, как из центра, раствором циркуля, равным АС, делаем насечку на стороне ВС. Обозначим эту точку К.
∆ КАС- равнобедренный с равными сторонами АК=АС.
Разделив КС пополам, получим точку М, в которой медиана ∆ КАС пересекается с основанием КС. Т.к. в равнобедренном треугольнике медиана=биссектриса=высота, отрезок АМ будет искомой высотой.
Для этого из точек К и С, как из центра, одним и тем же раствором циркуля ( больше половины КС) проведем две полуокружности. Соединим точки их пересечения с А.
Отрезок АМ разделил КС пополам и является искомой высотой ∆ АВС из вершины угла А.