Объяснение:
tg∠MCH=MH/CH
∆ABC - прямоугольный:
по теореме Пифагора:
АВ=√(ВС²+АС²)=√(15²+12²)=√369=3√41
по свойству медианы в прямоугольном тр-ке ,проведенной из вершины прямого угла:
СМ=АМ=МВ=1/2АВ=1/2×3√41=3/2×√41
S=1/2×AB×CH
CH=2S/AB
S=1/2×AC×BC=1/2×12×15=90
CH=2×90/3√41=60/√41=(60√41) /41
∆МНС -прямоугольный ,т.к СН-высота.
по теореме Пифагора:
МН=√(СМ²-СН²)=√((3/2×√41)²-(60/41×√41)²)=
=√(369/4-147600/1681)=√(369/4-3600/41)=
=√729/164=(27√41)/82
tg∠MCH=(27√41)/82:(60√41 )/41=
=27/82×41/60=27/2×1/60=27/120=9/40
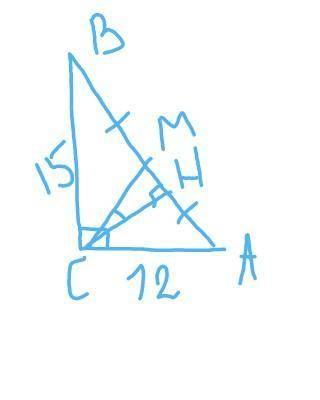
Відповідь: V = 18 куб. од.
Пояснення:
Запишемо рівняння даної площини 2х + 3у – 9z + 18 = 0 у відрізках .
Для цього поділимо рівняння на - 18 :
x/(- 9 ) + y/(- 6 ) + z/2 = 1 . Запишемо коорд. вершин тетраедра DOAB :
A(- 9 ; 0 ; 0 ) , B( 0 ;- 6 ; 0 ) , O( 0 ; 0 ; 0 ) , D( 0 ; 0 ; 2 ) . Об'єм його
обчислимо за формулою : V = 1/3 S oc * H .
| OA | = 9 ; | OB | = 6 ; | OD | = H = 2 . ΔOAB - прямокутний , тому
S oc = 1/2 * | OA | * | OB | = 1/2 *9 *6 = 27 ; S oc = 27 .
V = 1/3 * 27 * 2 = 18 ( куб. од. ) ; V = 18 куб. од.