
(МН·РН) = 4 ед.
(ОР·РК) = -2 ед.
Объяснение:
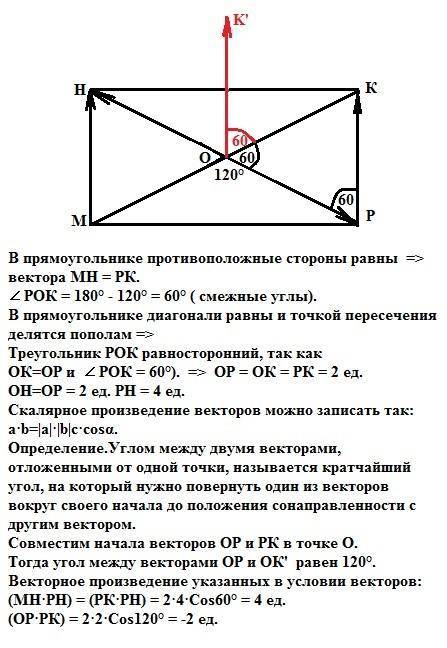
В прямоугольнике противоположные стороны равны =>
вектора МН = РК.
∠ РОК = 180° - 120° = 60° ( смежные углы).
В прямоугольнике диагонали равны и точкой пересечения делятся пополам =>
Треугольник РОК равносторонний, так как
ОК=ОР и ∠ РОК = 60°). => ОР = ОК = РК = 2 ед.
ОН=ОР = 2 ед. РН = 4 ед.
Скалярное произведение векторов можно записать так:
a·b=|a|·|b|c·сosα.
Определение: "Углом между двумя векторами, отложенными от одной точки, называется кратчайший угол, на который нужно повернуть один из векторов вокруг своего начала до положения сонаправленности с другим вектором".
Совместим начала векторов ОР и РК в точке О. Тогда угол между векторами ОР и ОК' (вектора ОК и ОК' равны) равен 120°.
Векторное произведение указанных в условии векторов:
(МН·РН) = (РК·РН) = 2·4·Cos60° = 4 ед.
(ОР·РК) = 2·2·Cos120° = -2 ед.
Что такое правильная четырехугольная призма с равными ребрами, мне не вполне ясно. По моему, это куб. Однако, если это не так, условие не полное...
В случае куба :))) СD1 II BA1, а отрезки ВА1 и А1С1 имеют общую точку А1. Угол между ними 60 градусов (КОСИНУС РАВЕН 1/2:)) потому что вместе с ВС1 они образуют равносторонний треугольник со стороной корень(2);
В случае, если боковые стороны ХХ1 (Х = А, В...) наклонны, боковые грани - ромбы, а не квадраты, и надо знать какой- то угол. Иначе ответ не получить.