Объяснение:
Проведем высоты как показано на рисунке. MN=BC=5 (т.к. BCNM - прямоугольник). BM=CN=h Обозначим AM как x, для удобства. AD=AM+MN+ND 20=x+5+ND ND=15-x Для треугольника ABM запишем теорему Пифагора: AB2=h2+x2 202=h2+x2 h2=400-x2 Для треугольника CDN запишем теорему Пифагора: CD2=h2+ND2 252=h2+(15-x)2 625=h2+(15-x)2 Подставляем вместо h2 значение из первого уравнения: 625=400-x2+(15-x)2 625-400=-x2+152-2*15*x-x2 225=152-2*15*x 225=225-30x 30x=0 x=0, получается, что BM совпадает со стороной AB, т.е. AB является высотой трапеции. Тогда площадь трапеции равна: S=AB(AD+BC)/2=20(20+5)/2=10*25=250
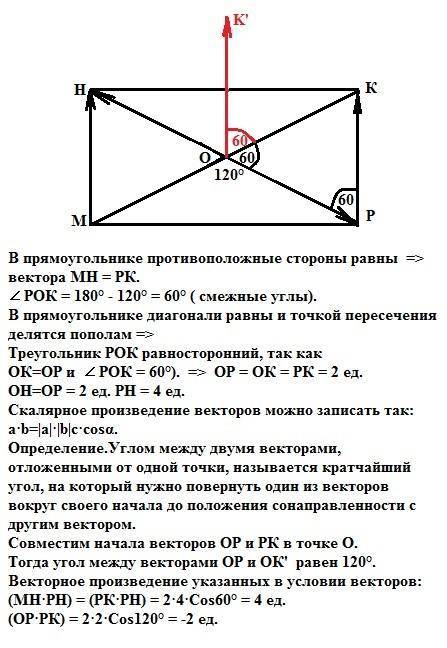
(МН·РН) = 4 ед.
(ОР·РК) = -2 ед.
Объяснение:
В прямоугольнике противоположные стороны равны =>
вектора МН = РК.
∠ РОК = 180° - 120° = 60° ( смежные углы).
В прямоугольнике диагонали равны и точкой пересечения делятся пополам =>
Треугольник РОК равносторонний, так как
ОК=ОР и ∠ РОК = 60°). => ОР = ОК = РК = 2 ед.
ОН=ОР = 2 ед. РН = 4 ед.
Скалярное произведение векторов можно записать так:
a·b=|a|·|b|c·сosα.
Определение: "Углом между двумя векторами, отложенными от одной точки, называется кратчайший угол, на который нужно повернуть один из векторов вокруг своего начала до положения сонаправленности с другим вектором".
Совместим начала векторов ОР и РК в точке О. Тогда угол между векторами ОР и ОК' (вектора ОК и ОК' равны) равен 120°.
Векторное произведение указанных в условии векторов:
(МН·РН) = (РК·РН) = 2·4·Cos60° = 4 ед.
(ОР·РК) = 2·2·Cos120° = -2 ед.
114°
Объяснение:
треугольник равнобедренный,углы при основании равны (углы NMK и NKM)
сумма всех углов треугольника 180°
угол NMK+ угол NKM= 180°-48°=132°
угол NMK=углу NKM= 132°/2 =66°
LMK развернутый угол, 180°
угол LMN=180°-66°=114°