Дано :
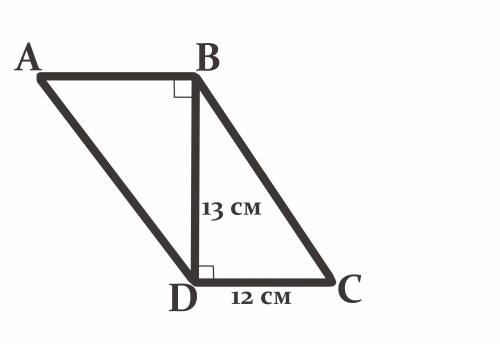
Четырёхугольник ABCD - параллелограмм.
Отрезок DB - диагональ = 13 см.
∠ABD = 90°.
CD = 12 см.
Найти :
S(ABCD) = ?
AB ║ CD (по определению параллелограмма).
Рассмотрим накрест лежащие ∠ABD и ∠BDC при параллельных прямых АВ и CD и секущей BD.
При пересечении двух прямых секущей накрест лежащие углы равны.То есть -
∠ABD = ∠BDC = 90°.
Тогда отрезок BD - ещё и высота параллелограмма ABCD (по определению).
Площадь параллелограмма равна произведению его стороны и высоты, опущенной на эту сторону.Следовательно -
S(ABCD) = BD*CD
S(ABCD) = 13 см*12 см
S(ABCD) = 156 см².
156 см².
1.60. Углы опираются на одну и ту же дугу, то есть вписанный угол равен половине центрального угла.
2.80. Аналогичная ситуация, только вписанный угол умножаем на 2, и получаем центральный.
3.90. АС- диаметр, который делит окружность пополам, то есть дуга равна 180, а угол 90.
4.140. Угол 40 умножаем на 2, чтобы узнать дугу, потом из 360 (вся окружность) вычитаем 80, получаем 240 (большая дуга, на которую опирается искомый угол), то есть 240 делим на 2, и узнаём угол.
5.125. Аналогично 4.360-110=250, 250:2=125.
6.160. Аналогично 4,5. 100*2=200, 360-200=160.
7.30. углы опираются на одну и ту же дугу.