а - сторона ромба
периметр
Р = 4а = 52
а = 52/4 = 13 см
Диагонали ромбы d1 и d2 перпендикулярны =>
d1 / d2 = 5 / 12 или d1 = 5d2 / 12
Cтороны прямоугольных треугольников, образуемых диагоналями,будут ^
d1/2, d2/2 -катеты
а - -гипотенуза (она же сторона ромба)
По теореме пифагора
(d1/2)^2 + (d2/2)^2 = a^2
d1^2 + d2^2 = 4a^2
(5d2 /12)^2 + d2^2 = 13^2
25d2^2 + 144d2^2 = 13^2 * 12^2
169d2^2 = (13^2*12^2
13^2 d2^2 = 13^2 * 12^2
d2^2 = 12^2
d2 = 12 см - вторая диагональ
d1 = 5d2 / 12 = 5 * 12 / 12 = 5 - первая диагональ
ответ: диагонали d1=5 cм, d2 = 12 см
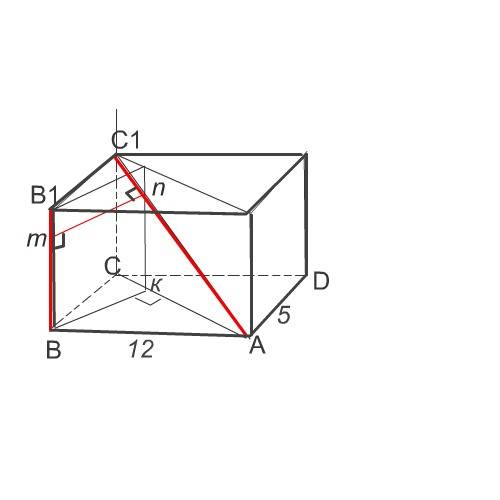
Расстоянием между скрещивающимися прямыми называется длина их общего перпендикуляра.
На рисунке это прямые BB1 и AC1 и их общий перпендикуляр mn.
или
Расстоянием между скрещивающимися прямыми называется расстояние между одной из скрещивающихся прямых и плоскостью, проходящей через другую прямую параллельно первой
На рисунке это прямая BB1 и плоскость СС1А1А, содержащая прямую АС1
mn=ВК как параллельные прямые (mn параллельна плоскости основания, а ВК - проекция mn на плоскость основания)
Искомое расстояние - высота ВК треугольника АВС основания.
АВ =12,
ВС=АD=5
АС=√ (12²+5²)=13 см
Катет прямоугольного треугольника есть среднее пропорциональное между
гипотенузой и отрезком гипотенузы, заключенным между катетом и высотой.
Пусть отрезок СК=х.
Тогда
5²=13*х
х=СК=25/13 см
ВК=√(ВС²-СК²)=√(25-625/169)=60/13=4 ⁸/₁₃ см
А) по гипотенузе и острому углу