ответ: 12 (ед. длины)
Объяснение:
Одна из формул биссектрисы треугольника
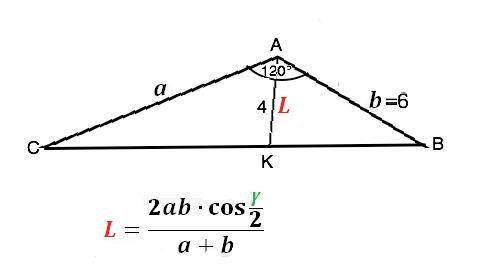
L={2ab•cos(0,5γ)}:(a+b) ,
где L биссектриса, а и b- стороны, γ - угол между ними.
На приведенном рисунке АК - биссектриса ∆ АВС, АС=а, АВ=6, угол А=γ =120°
cos0,5γ=cos60°=1/2
4=2a•6•0,5/(a+6) =>
4a+24=6a =>
АС=a=12 (ед. длины)
Или с тем же результатом найти:
1) По т. косинусов из ∆ АКВ найти КВ
2) по т. синусов из ∆ АКВ угол В
3) из суммы углов треугольника угол С
4) по т. синусов вычислить длину искомой стороны АС
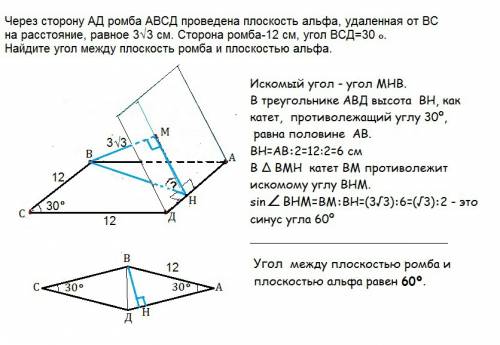
Через сторону АД ромба АВСД проведена плоскость альфа, удаленная от ВС на расстояние, равное 3√ 3 см. Сторона ромба-12 см, угол ВСД=30º. Найдите угол между плоскость ромба и плоскостью альфа
ВС ║АД, ⇒ ВС║α
АД ∈ плоскости α, и расстояние от ВС до плоскости равно длине отрезка их общего перпендикуляра (свойство).
Угол между плоскость ромба и плоскостью α -двугранный угол, и его величина определяется градусной мерой линейного угла.
В данном случае это величина угла, который получится, если из точки Н к АД— линии пересечения плоскости ромба и плоскости альфа, —провести перпендикуляры в обеих плоскостях.
Пусть Н - основание высоты ромба, проведенной из В к АД, а НМ перпендикуляр к АД в плоскости альфа. (см. рисунок)
Искомый угол - угол МНВ.
В треугольнике АВД высота ВН как катет, противолежащий углу 30º, равна половине гипотенузы АВ.
ВН=АВ:2=12:2=6 см
В ∆ ВМН катет ВМ противолежит искомому углу ВНМ.
sin∠ВНМ=ВМ:ВН=(3√3):6=(√3):2 - это синус угла 60º
Угол между плоскость ромба и плоскостью альфа равен 60º.
Дано: ABCD - квадрат, EFGH - прямокутник, Sabcd= Sefgh, AB= 8 см, FG= 16 см.
Знайти: EF.
Розв'язання.
Знайдемо площу квадрата.
Sabcd= AB²= 8•8= 64 (см²).
Оскільки за умовою площа ABCD дорівнює площі EFGH, то Sefgh= 64 см² відповідно.
Площа прямокутника дорівнює добутку двох його суміжних сторін, тобто:
Sefgh= EF•FG;
64= EF•FG;
64= EF•16;
EF= 64 : 16;
EF= 4 (см).
Отже, друга сторона прямокутника дорівнює 4 см.
Відповідь: 4 см.