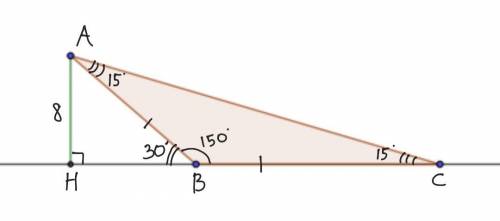
Дано: ΔABC - равнобедренный, АС - основание, АВ=ВС, ∠В=150°, АН - высота, АН = 8 е.д.
Найти: BC.
Решение.
Поскольку треугольник тупоугольный, а высота проведена из острого угла, то высота принадлежит продолжению противолежащей стороны.
Поэтому рисуем продолжение прямой ВС и высоту АН, проведённую к нему.
В ΔАНВ: ∠НВА = 180°-150°= 30° (как смежные).
АНВ - прямоугольный треугольник (АН ведь высота) с гипотенузой АВ.
В прямоугольном треугольнике, если острый угол равен 30°, то противолежащий этому углу катет равен половине гипотенузы.
АН=½АВ.
АВ= 2АН.
АН по условию 8, тогда АВ= 2×8=16.
ΔАВС - равнобедренный, АВ=ВС. Значит, ВС=16 е.д.
ответ: 16 е.д.
Объяснение:
1)ΔАВС, ∠С=90°,∠А=47°.
Сумма острых углов в прямоугольном треугольнике 90°⇒∠В=90°-47°=43°. ответ 43°.
2)ΔАВС, ∠С=90°,∠А=30°, АВ=16 см.
В прям. треугольнике катет , лежащий против угла 30° раен половине гипотенузы, т.е. СВ=1/2*ВА , СВ=8 см.
4)ΔСВD, ∠С=90°,ВD=14 см, СВ=7 см , СК⊥ВD. Найти ∠ВСК.
ΔСВD-прямоугольный и катет СВ равен половине гипотенузы ( 7*2=14 ) . Значит ∠СDВ=30° .Тогда ∠В=90°-30°=60°
Т.к. СК⊥ВD , то ΔСКВ-прямоугольный . Угол ∠ВСК=90°-60°=30°