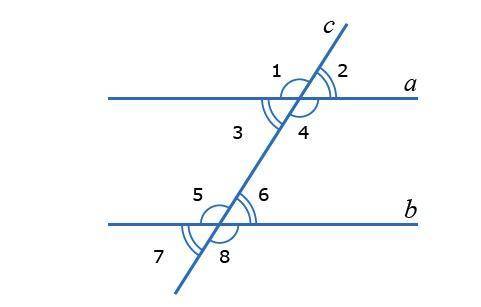
∠2=∠3=∠6=∠7=65°
∠1=∠4=∠5=∠8=115°
Объяснение:
∠1 и ∠2 - смежные углы. Их сумма равна 180°
Пусть ∠2=х°, тогда ∠1=(х+50)°, их сумма 180°:
х+х+50=180
2х=130
х=65°
∠2=65°, ∠1=115°
∠3=∠2 - как вертикальные углы. ⇒∠3=65°
∠6=∠3 - как внутренние накрест лежащие углы при параллельных прямых а и b и секущей с. ⇒ ∠6 = 65°
∠7=∠6 - как вертикальные углы ⇒ ∠7=65°
∠4=∠1 - как вертикальные углы. ⇒∠4=115°
∠5=∠4 - как внутренние накрест лежащие углы при параллельных прямых а и b и секущей с. ⇒ ∠5 = 115°
∠8=∠5 - как вертикальные углы ⇒ ∠8=115°
Кроме того, S трапеции равна полусумме оснований на высоту, которая у нас равна двум радиусам ⇒ S=(a+b)R⇒a+b=S/R; c=S/(2R).
Совершив стандартную процедуру - опустив высоты из вершин верхнего основания на нижнее, разбиваем нижнее на три отрезка, средний из которых равен b, а крайние равны (a-b)/2.
Один из таких отрезков вместе с боковой стороной и высотой образуют прямоугольный треугольник, из которого находим нижний катет (я там уже избавился от двойки в знаменателе):
a-b=2√(S^2/(4R^2)-4R^2)=√(S^2-16R^2)/R
Вспомнив a+b=S/R, получаем формулы для a и b:
a=(S+ √(S^2-16R^2))/(2R);
b=(S- √(S^2-16R^2))/(2R)