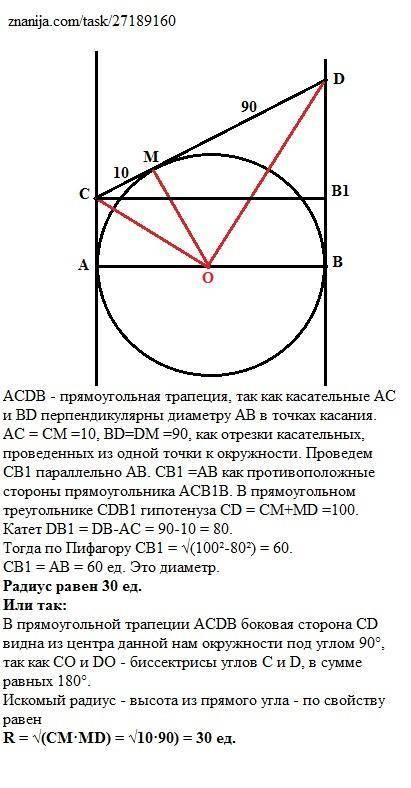
R = 30 ед.
Объяснение:
ACDB - прямоугольная трапеция, так как касательные АС и BD перпендикулярны диаметру АВ в точках касания.
АС = СМ =10, BD=DM =90, как отрезки касательных, проведенных из одной точки к окружности.
Проведем СВ1 параллельно АВ.
СВ1 =АВ как противоположные стороны прямоугольника АСВ1В. В прямоугольном треугольнике CDB1 гипотенуза CD = СМ+MD =100 ед.
Катет DB1 = DB-АС = 90-10 = 80ед.
Тогда по Пифагору СВ1 = √(100²-80²) = 60ед.
СВ1 = АВ = 60 ед. Это диаметр.
Радиус равен 30 ед.
Или так:
В прямоугольной трапеции АСDB боковая сторона CD видна из центра данной нам окружности под углом 90°, так как СО и DО - биссектрисы углов C и D, в сумме равных 180°.
Искомый радиус - высота из прямого угла - по свойству равен
R = √(CM·MD) = √10·90) = 30 ед.
а) сс1; б) а1с; в) bc1 = d1c1 - d1b.
Объяснение:
Правила:
СУММА. Начало второго вектора совмещается с концом первого, начало третьего — с концом второго и так далее, сумма же n векторов есть вектор, с началом, совпадающим с началом первого, и концом, совпадающим с концом n-го (то есть изображается направленным отрезком, замыкающим ломаную).
РАЗНОСТЬ. Для получения вектора разности (c) = (a-b) начала векторов соединяются и началом вектора разности (c) будет конец вектора (b) (вычитаемое), а концом — конец вектора (a) (уменьшаемое).
Тогда:
Вектор ca1+ad+d1c1 = ca1+a1d1+d1c1 = сс1 (вектор ad = вектору а1d1)
Вектор ab-aa1-c1b1 = a1b-c1b1 = d1c-d1a1 = a1c (вектор a1b = вектору d1c).
Вектор bc1 = d1с1 - d1b