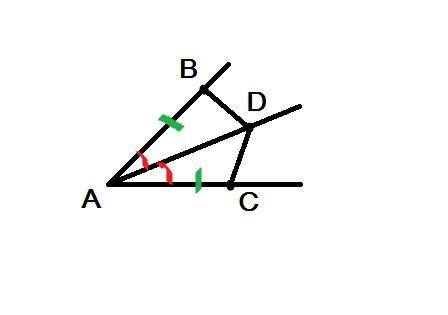
Данные треугольники имеют две пары равных углов ∡1 и ∡2, ∡3 и ∡4, каждый из которых прилежит к общей стороне АС треугольников. Значит, данные треугольники равны по второму признаку (сторона и два прилежащих угла).
№2У данных треугольников две пары равных сторон DC=AD и АВ=ВС. Также треугольники имеют общую сторону ВD, из чего делаем вывод: треугольники равны по третьему признаку (три стороны).
№3Указанные треугольники имеют равные стороны ОD=ОС и АО=ВО. Также имеем пару вертикальных углов ∡DOА и ∡ВОС. Они равны по своему свойству. Значит, треугольники равны по первому признаку (две стороны и угол между ними).
№4Из условия мы знаем, что АВ=АС (...отложены равные отрезки...) и ∡ВАD=∡CFD (биссектриса). Также АD - общая сторона. Значит, треугольники равны по двум сторонам и углу между ними.
Угол между плоскостями - это линейный угол, образованный сечением этих плоскостей плоскостью, перпендикулярной к их линии пересечения.
В нашем случае это угол DHD1, где DH и HD1 - перпендикуляры к АВ. В прямоугольном треугольнике DHD1 с прямым углом D1 катет HD1 равен HD1=HD*Cosβ. Cosβ=√(1-sin²β)=√(1-1/16)=√15/4. Тогда HD1=((9*√5)/4)*(√15/4)=45√3/16. Площадь параллелограмма равна S=a*h, где а - сторона параллелограмма, а h - высота, опущенная на эту сторону. В нашем случае а=9, h=45√3/16.
S=9*45√3/16=405√3/16