1)Sabc=1/2*2*2√3=2√3(по формуле S прямоугольного треугольника)
2)Тут два варианта(находим сторону AC)
Первый : треуг. ABC-прямоугольный:
по т. Пифагора: АС^2=(2√3)^2+4=16. АС=4
Второй : угол ВАС=30° в прямоугол треуг АВС. Отсюда по св-ву
АС=2ВС=4
3)треуг ДАС: по т о сумме углов треугольника: угол СДА+угол ДСА+угол САД=180°. Отсюда угол САД=45°=угол СДА-по призн треуг СДА-р/б треугольник-по опр АС=СД =4
4)Sсda=4*4*1/2=8(по формуле S прямоугольного треугольника)
5)Sabcd=Sсda+Sabc=8+2√3
ответ: 8+2√3
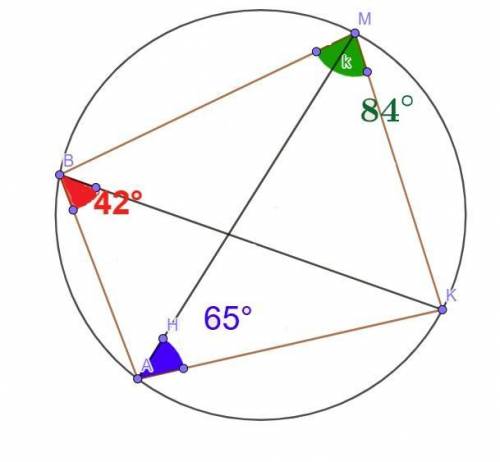
∠А (∠ВАК) = 96°
∠К (∠АКМ) = 73°
∠М (∠ВМК) = 84°
∠В (∠АВМ) = 107°
Объяснение:
Сума протилежних кутів вписаного у коло чотирикутника дорівнює 180 градусам (властивість).
∠ВМК+∠ВАК = 180°
∠ВАК = 180° - ∠ВМК = 180° - 84° = 96°
∠АВК та ∠АМК - вписані кути. Вони спираються на дугу АК.
Вписані кути, що спираються на одну дугу, рівні. ⇒
∠АМК = ∠АВК= 42°
Так як сума кутів трикутника дорівнює 180°, то з ΔАМК знаходимо кут ∠АКМ:
∠КАМ+∠АМК+∠АКМ = 180°
∠АКМ = 180°- ∠КАМ-∠АМК= 180°-65°-42°= 73°
Так як Сума протилежних кутів вписаного у коло чотирикутника дорівнює 180 градусам, маємо:
∠АВМ + ∠АКМ = 180°
∠АВМ = 180° - ∠АКМ = 180°- 73° = 107°
Пусть даны два отрезка а и m и угол α. Надо построить ΔАВС такой, что ВС = а, ΔBCD АВ + АС = m.
Решение возможно лишь при а < m т.к. сумма любых двух сторон треугольника больше третьей стороны.
Построим ΔBCD по двум сторонам (BD = m, ВС = а) и углу между ними (∠В = α).
Проведем серединный перпендикуляр от CD, он пересечет BD в точке А. AD = АС. Получаем искомый ΔBCD, где ВС = а, ΔBCD В = α, АВ + АС = m, т.к. АС = AD.
Если m = а, то в ΔBCD ∠С будет больше ∠D. Серединный перпендикуляр d к стороне CD по теореме 1.1. должен пересекать либо сторону ВС, либо СD.
Докажем, что серединный перпендикуляр пересекает именно BD.
Допустим, d пересекает сторону ВС в точке М, а прямую BD в точке K. Т.к. KD > BD, то ∠KCD < ∠BCD.
По свойству серединного перпендикуляра ΔDKC — равнобедренный, таким образом, ∠KCD = ∠D, но тогда ∠D > ∠BCD (т.к. m > a), то есть в ΔBCD ∠D < ∠С. Противоречие, т.е. d пересекает именно ВD.
Таким образом, задача имеет единственное решение.