8√3
Объяснение:
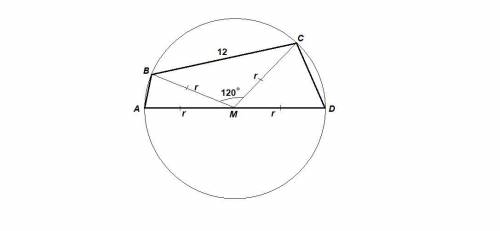
MA = MB = MC = MD, значит М - центр описанной около четырехугольника окружности.
Если четырехугольник вписан в окружность, то суммы противолежащих углов равны 180°.
∠А = 180° - ∠С = 180° - 95° = 85°
∠D = 180° - ∠B = 180° - 115° = 65°
ΔАВМ равнобедренный, значит углы при основании АВ равны, ⇒
∠АМВ = 180° - 2∠А = 180° - 2 · 85° = 180° - 170° = 10°
ΔMCD равнобедренный, значит углы при основании CD равны, ⇒
∠CМD = 180° - 2∠D = 180° - 2 · 65° = 180° - 130° = 50°
∠ВМС = 180° - (∠АМВ + ∠CМD) = 180° - 60° = 120°
ΔВМС: по теореме косинусов:
BC² = MB² + MC² - 2·MB·MC·cos120°
144 = r² + r² - 2 · r · r · (-1/2)
144 = 2r² + r²
3r² = 144
r² = 48
r = 4√3
AD = 2r = 8√3
Средняя линия треугольника параллельна стороне треугольника и равна ее половине . В условии не сказано, параллельно какой из сторон проведена средняя линия MN, поэтому может быть два варианта решения.
1 вариант:
MN параллельна основанию RS, RF=SF, RS+2*RF=30 (дано). Тогда
RS=8, а RF=(30-8):2=11.
2 вариант:
MN параллельна боковой стороне RF. Тогда
RF=SF=8, а RS=30-2*8=14.
Оба варианта удовлетворяют условию существования треугольника (теорема о неравенстве), так как большая сторона меньше суммы двух других сторон.
Объяснение: