ответ
ответ дан
ivanproh1
S = 102 см²
Объяснение:
Диагонали ромба взаимно перпендикулярны и точкой пересечения делятся пополам. Получается четыре прямоугольных треугольника, в которых гипотенузы равны стороне ромба, а катеты - половинам диагоналей. Тогда по Пифагору 26²= Х² +(Х-14)², где Х - половина большей диагонали. Из этого уравнения находим
Х = 7±√(49+240) = 17см.
Тогда половина меньшей диагонали равна 17-14 = 3см и площадь одного треугольника равна (1/2)*17*3 = 25,5см². Таких треугольников в ромбе четыре.
Площадь ромба равна 4*25,5 = 102см².
Можно через диагонали:
S=(1/2)*D*d = (1/2)*34*6 = 102 см².
Две прямые дороги KM и PN, которые пересекаются где-то за лесом в недоступной точке С. Нужно найти расстояние от некоторого пункта А на дороге КМ к точке С пересечения дорог. Для этого обозначили на дороге PN пункт В так, чтобы можно было измерить расстояние АВ, и определили углы ВАМ и ABN. Объясните нахождения расстояния АС. Вычислите АС, если АВ = 800 м , ∠ВАМ = 85°, ∠АВN = 52° .
Объяснение: Таким , зная определенные теоремы геометрии, можно не ходить часами с линейкой по дороге измеряя длину АС, а ВЫЧИСЛИТЬ ее по теореме синусов .
Теорема синусов :" Стороны треугольника пропорциональны синусам противолежащих углов."
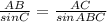. Видимый и измеряемый отрезок пути АВ=800 м. Угол ∠С вычисляется по т. о сумме углов треугольника, т.к два доступных угла можно измерить на местности с простейшей астролябии ( можно изготовить в домашних условиях) : ∠С=180°-85°-52°=43°.
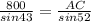, АС=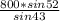 
≈ 
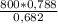≈ 924 (м).
1.
Дано:
Прямоугольный треугольник АВС. Угол С=90*, угол А=37*.
Найти: Угол В.
Угол А и В острые. По первому свойству мы можем найти угол В.
Свойство:
Сумма двух острых углов прямоугольного треугольника равна 90*.
Получается:
Угол В=90*-37*=53*
ответ: 53*.
2.
Дано: прямоугольный треугольник АВС.
Угол С=90*, угол А=30*.
АВ=15см.
Найти: катет ВС.
Катет ВС, мы можем найти по второму свойству:
Катет прямоугольного треугольника, лежащий против угла в 30*, равен половине гипотенузы.
Получается, чтобы найти катет ВС, нам надо:
15:2=7,5
Катет ВС=7,5см.
ответ: 7,5см.
3.
Дано:
Прямоугольный треугольник АВС. Угол В=90*, С=30*. Катет АВ=4см.
Найти: Гипотенузу АС.
Так как АВ лежит под углом в 30*, получается, чтобы найти АС, надо:
4*2=8
Гипотенуза АС=8см.
ответ: 8см.
4.
Дано:
Прямоугольный треугольник АВС. Угол В=90*. АС=8,4см. АВ=4,2см.
Найти: Угол А и угол С.
Гипотенуза АС=8,4см, а катет АВ равен половине гипотенузы АС.
Получается мы можем найти угол С по третьему свойству:
Если катет прямоугольного треугольника равен половине гипотенузы, то угол, лежащий против этого катета равна 30*.
Угол А мы сможем найти по первому свойству:
Сумма острых углов прямоугольного треугольника равен 90*.
Получается:
Угол А=90*-30*=60*
ответ: 30*; 60*.