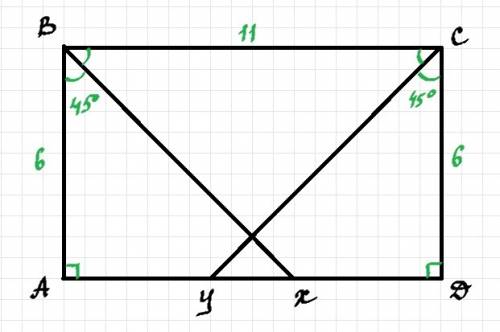
Рисунок к задаче в прикрепленном файле.
Рассмотрим ΔАВХ и ΔDCY.
Они прямоугольные, т.к. в прямоугольнике все углы прямые и ∠А=∠D=90°. АВ=CD, т.к. в прямоугольнике противоположные стороны равны. ∠АВХ=∠YCD, т.к. ВХ и CY биссектрисы и делят прямые углы В и С пополам (∠СВХ=∠ХВА=∠BCY=∠YCD=45°).
Следовательно ΔАВХ=ΔCDY (по катету и прилежащему острому углу). Эти треугольники равнобедренные, т.к. углы при основании у них равны.
АВ=АХ=YD=DC=6 (см).
АХ+YD=6+6=12 (см).
ВС=АD=11 см.
YX=АХ+YD-ВС=12-11=1 (см).
ответ: YX=1 см.
а) Из условия следует, что угол ВМК должен быть равен углу А. В треугольниках МВК и АВС угол В общий. Треугольники подобны по двум углам (первый признак подобия) . Следовательно, КМ: АС=ВК: ВС
б) Площадь треугольника АВС равна сумме площадей четырёхугольника AKMC (S1) и площади треугольника МВК (S2). Значит, площадь треугольника АВС относится к площади треугольника МВК как 9:1. Отношение площадей подобных фигур равно квадрату коэффициента подобия. 9=3^2. Коэффициент подобия равен 3. Тогда АВ: ВМ=3
Объяснение: