Доказано. См ниже
Объяснение:
Продлим СК за точку К до пересечения с прямой AD в точке Т.
Обозначим KA=LC=a , КВ=b , BL=c.
Для доказательства используем теорему, если в треугольнике TCD выполняется соотношение CD/DT=CE/ET тогда DE является биссетрисой угла D.
Рассмотрим треугольники КВС и КАТ. Они подобны по 2-м углам.
Тогда КВ/KA=BC/AT => b/a =(a+c)/AT=> AT= a(a+c)/b (1)
Рассмотрим треугольники ELC и EАТ. Они подобны по 2-м углам.
=> CE/TE=LC/AT= a*b/(a*(a+c)) = b/(a+c)
Рассмотрим теперь отношения CD:DT
CD=a+b
DT=a+c+AT=(b(a+c)+a(a+c))/c = (a+b)(a+c)/b
CD:DT=(a+b): ((a+b)(a+c)/b)=b/(a+c)
Таким образом СЕ:ТЕ= CD:DT=b/(a+c) , что и требовалось доказать.
Таким образом DO - биссектриса угла D
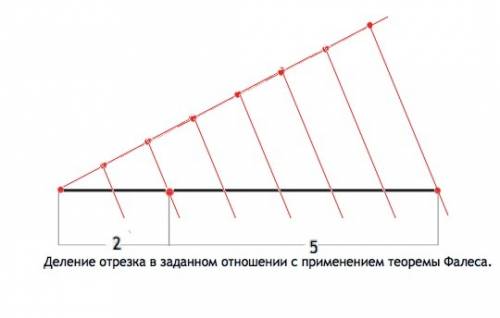
Для решения применим теорему Фалеса: Если на одной из двух прямых отложить последовательно несколько отрезков и через их концы провести параллельные прямые, пересекающие вторую прямую, то они отсекут на второй прямой пропорциональные отрезки.
Чтобы без линейки с делениями разделить отрезок, длина которого не известна, нужно от одного из концов этого отрезка провести под углом к нему вс луч и на этом луче на равном расстоянии отметить нужное количество точек.
а) На вс луче отложим через равные промежутки 2+5 =7 точек. Затем через последнюю точку и конец заданного отрезка проведём прямую и через все точки ещё 6 прямых, параллельных ей. При этом заданный отрезок будет разделен на 7 равных частей. Отсчитаем 2 из получившихся отрезков. Остальная часть равна 5 отмеренным отрезкам, а исходный разделен в отношении 2:5
Можно на заданном отрезке откладывать не 7 отрезков, а провести всего 2 прямые - через седьмую и параллельно ей через вторую точку. Заданный отрезок будет разделён в нужном отношении.
б) и в) делим точно так же.
Відповідь А(-3;0)
Объяснение: