α = 45°
Объяснение:
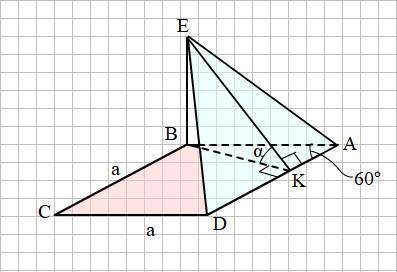
Смотри прикреплённый рисунок.
Из вершины В ромба проводим высоту ВК.
ВК = а · sin A = a · sin 60° = 0.5a√3.
Соединим точку Е с точкой К. ВК является проекцией наклонной ЕК на плоскость АВСD. Поскольку ВК - высота ромба. то ВК ⊥ AD.
По теореме о трёх перпендикулярах: если AD ⊥ BK (проекции наклонной ЕК), то AD⊥ ЕК. Следовательно, ∠ЕКВ = α является линейным углом, служащим мерой двугранного угла между плоскостями ADE и АВСD.
Найдём этот угол.
tg α = BE : BK = 0.5a√3 : 0.5a√3 = 1.
Следовательно, ∠α = 45°
1.√(36+64)=√100=10
√(64+36)=√100=10
√(144+256)=√400=20
√(256+144)=√400=20
чтобы по координатам найти длину вектора, надо
1) возвести в квадрат координаты;
2) сложить эти квадраты;
3) извлечь корень квадратный из суммы квадратов координат.
2. →u=3→а-2→b={-24;27}-{18;-14}{-42;-41} ,
→v=2→a+→b={-16;18}+{9;-7}={-7;11}
3. {-27;9}-{-27;18}={0;-9}
чтобы найти сумму или разность векторов, нужно сложить или вычесть их соответствующие координаты, чтобы умножить вектор на число, надо на это число умножить все координаты.