Так как все углы данного шестиугольника равны, он - выпуклый.
Сумма углов выпуклого многоугольника вычисляется по формуле N=180°•(n-2), где n- количество его вершин.
N=180°•(6-2)=720°
Каждый из равных углов равен 720°:6=120°
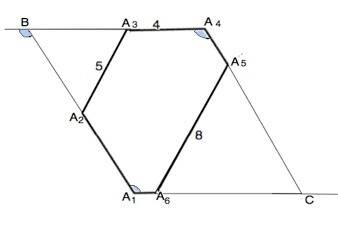
Продлим стороны А1А2 и А4А2 до пересечения в точке В, и стороны А4А5 и А1А6 до пересечения в точке С.
Внешние углы при внутренних, равных 120°, равны 180°-120°=60°.
Тогда углы в ∆ А2ВА3 и ∆ А5СА6 - равны 60°, стороны ∆ А2ВА3 равны 5, стороны ∆ А5СА6 равны 8.
Внешний угол при вершине В=внутреннему углу А1=120°
Эти углы соответственные. Из равенства соответственных углов следует параллельность А4В║А1С.
Внешний угол при вершине В=внутреннему углу А4=120°.
Эти углы соответственные, из чего следует параллельность ВА1║А4С.
⇒ В четырехугольнике ВА4СА1 противоположные стороны параллельны. ВА4СА1 - параллелограмм, ⇒его противоположные стороны равны. Следовательно, ВА4=5+4=9
А1С=ВА4=9.
Сторона А1А6=9-А6С=9-8=1
Проекции катетов на гипотенузу прямоугольного треугольника - это отрезки гипотенузы, на которые ее делит высота, т.к. высота - перпендикуляр к прямой ( гипотенузе), а катеты – наклонные из вершины прямого угла.
Катет - среднее пропорциональное между гипотенузой и его проекцией на неё .
В треугольнике на рисунке приложения
Катет Вс=30 см, а ВН=18 - его проекция на гипотенузу.
BC²=АВ•НВ
900=АВ•18
АВ=900:18=50 см
Высота, проведенная к гипотенузе, делит прямоугольный треугольник на подобные. Из подобия следует отношение:
АН:АС=АС:АВ
АН=50-18=32
32:АС=АС:50 ⇒ АС²=32•50
АС=√1600=40 см
-----------
Если обратить внимание на отношение катета и гипотенузы 3:5 в ∆ ВСН, увидим, что этот треугольник - египетский. Отсюда следует АВ=50 см, (т.к. меньший катет=30). а АС=40 см. Получим длины сторон треугольника, отношение которых 3:4:5.

Угол DBC =66°
Объяснение:
На фото и рисунок и объяснение