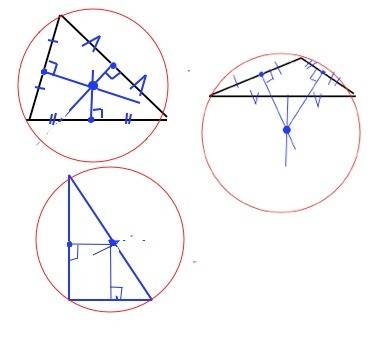
Центром описанной окружности треугольника является точка пересечения срединных перпендикуляров.
Для остроугольного треугольника этот центр будет в треугольнике.
Построение.
Построить нужный треугольник не составляет труда.
1) Для остроугольного треугольника центр описанной окружности будет внутри треугольника. .
Измерьте линейкой каждую сторону треугольника и найдите ее середину. С угольника ( у него есть прямой угол) проведите из середины каждой стороны прямые. Точка их пересечения - искомый центр описанной окружности.
Расстояние от него до вершин треугольника равны радиусу описанной окружности.
2) Для тупоугольного треугольника построение будет таким же, но срединные перпендикуляры пересекутся ВНЕ треугольника.
3) Для прямоугольного треугольника достаточно найти середину гипотенузы, т.к. срединные перпендикуляры пересекаются именно в этой точке. Полезно запомнить, что центром описанной вокруг прямоугольного треугольника окружности является середина его гипотенузы, т.к. расстояния от нее до вершин треугольника равны.
Как это выглядит, дано в приложении.
1. Утрержднние, справедливость которого устанавливается путем рассуждений.
2. Сумма длин сторон треугольника.
3. Отрезок, соединяющий вершину треугольника с серединой противоположной стороны.
4. Отрезок, соединяющий центр с какой-либо точкой окружности.
5. Часть плоскости, ограниченная окружностью.
6. Равные стороны равнобедренного треугольника.
7. Инструмент, используемый для построения окружностей.
8. Геометрическая фигура, состоящая из всех точек, расположенных на заданном расстоянии от данной точки.
9. Отрезок, проведенный под прямым углом к прямой.
10. Третья, не равная сторона равнобедренного треугольника.
11. Отрезок биссектрисы угла треугольника, соединяющий вершину треугольника с точкой противоположной стороны
Контрольное слово по вертикали - название изученной главы.