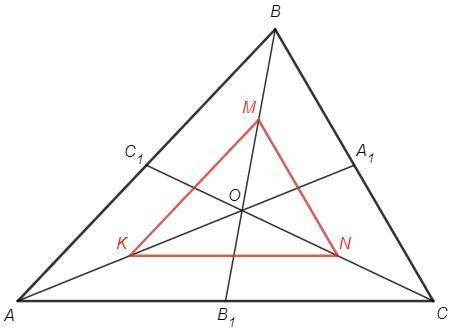
Средняя линия треугольника соединяет середины двух сторон, параллельна третьей стороне и равна ее половине.
Отрезки KM, MN, KN являются средними линиями в треугольниках AOB, BOC, AOC.
a) KM||AB, MN||BC, KN||AC
KMN~ABC по трем параллельным сторонам
б) KM=AB/2, MN=BC/2, KN=AC/2
P(ABC) =2P(KMN) =44*2 =88 (см)
в) Отношение соответствующих отрезков (медиан, биссектрис, высот и любых отрезков, построенных сходным образом) в подобных треугольниках равно коэффициенту подобия.
k=AB/KM =2
Медианы ABC вдвое больше медиан KMN.
Т.к. точка D равноудалена от сторон, то расстояния эти до сторон - ни что иное, как радиусы вписанной в треугольник окружности, центр которой находится в точке пересечения биссектрис, т.е. D -центр вписанной окружности. Ясно, что самая длинная сторона будет лежать против наибольшего угла, т.е. угла 77°, а тогда, используя, что есть величины углов оставшихся, данный искомый угол можем найти как
180°-38°/2-65°/2=161°-32°30'=128°30'
ответ 128°30'