Тема «Теорема о произведении отрезков пересекающихся хорд» (стр 170)
2. Решить три задачи:
1.Хорды КМ и ВС пересекаются в точке А. Найдите: а) АС, если ВА = 6,
АК = 2, АМ = 4; б) АК, если ВА = 0,8, АС = 0,7, АМ = 0,3; в) АВ, если
ВС = 16, АК = 9, АМ = 4.
2. Диаметр АВ окружности перпендикулярен к хорде СЕ и пересекает
ее в точке М. Найдите СЕ, если ВМ = 12 см, АМ = 6
3. При решении следующей задачи надо воспользоваться
утверждением, данным в № 670.
Через точку А проведены касательная АВ (В – точка касания) и секущая,
которая пересекает окружность в точках К и М (точка М находится
между точками А и К). а) Найдите КМ, если АМ = 6, АВ = 8;
б) найдите КМ, если АК = 15, АВ = 6.
Рисунки к задачам делаем обязательно. Работа рассчитана на 1 урок.
1)
Призма прямая, поэтому боковыми гранями будут прямоугольники. Одна их сторона это боковое ребро, а другая сторона это сторона основания. Найдём площадь боковой поверхности призмы как сумму площадей прямоугольников, которые составляют бок. пов.
S = 4см · 3см + 4см · 5см + 4см · 6см =
= 4см · (3см+5см+6см) = 4см · 14см = 56см².
ответ: 56см².
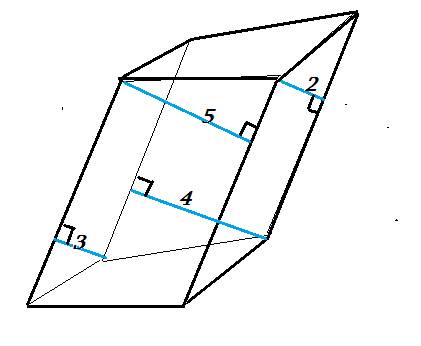
2)
Расстоянием между боковыми рёбрами призмы будет длина отрезка заключенного между боковыми рёбрами и лежащий на общем перпендикуляре. Боковые рёбра наклонной призмы это параллелограммы у которых мы знаем одну сторону (бок. реб.) и высоту проведённую к этой стороне (расстояние между бок. реб.), поэтому мы можем найти площадь параллелограмма. Площадь боковой поверхности найдём как сумму площадей параллелограммов, которые составляют бок. пов.
S = 8см · 3см + 8см · 4см + 8см · 5см =
= 8см · (3см + 4см + 5см) = 8см · 12см = 96см².
ответ: 96см².