На сколько я понял требуется решить только первую задачу.
Дана трапеция ABCD, AB=CD=7√2 см; AC⊥BD.
Найти радиус описанной около ABCD.
Пусть AC∩BD=F и пусть ∠FAB=α.
Вокруг равнобедренной трапеции всегда можно описать окружность!
ΔABD=ΔDCA по двум сторонам и углу между ними (AB=DC; AD - общая; ∠BAD=∠CDA), поэтому ∠ADB=∠DAC, как углы лежащий напротив равных сторон в равных треугольниках.
В ΔAFD:
∠AFD=90°; ∠FAD=∠FDA=(180°-∠AFD):2=90°:2=45°. Таким образом ΔAFD - равнобедренный прямоугольны, AF=DF.
В прямоугольном ΔAFB:
AF=AB·cosα=7√2·cosα см
BF=AB·sinα=7√2·sinα см
В ΔABD:
BD=BF+FD=BF+AF=7√2·(sinα+cosα) см
∠BAD=α+45°
Вокруг ΔABD описана таже окружность, что и вокруг трапеции.
По теореме синусов: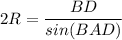 
, где R - радиус описанной.
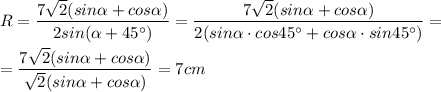
ответ: 7 см.
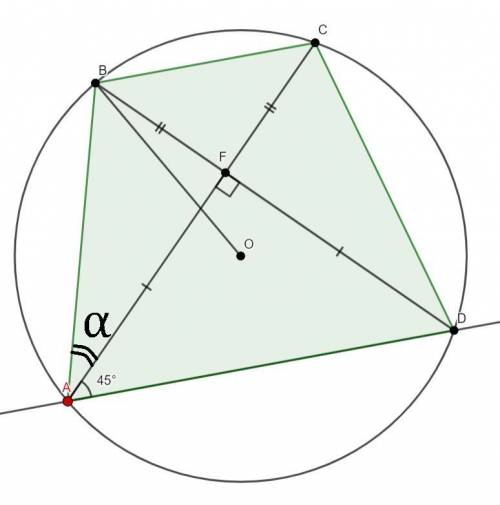
Окружность, вписанная в правильный многоугольник, и окружность, описанная около него, имеют общий центр, причем, так как стороны многоугольника - касательные для вписанной окружности, её радиус является высотой равнобедренного треугольника соединяющего центр с вершинами описанного многоугольника. (см. рисунок).
На рисунке О - центр окружностей, ОА=ОВ=R=8, ОН=r=4√3. Треугольник ОНВ прямоугольный. Sin∠OAH=ОН:ОА=4√3:8=√3/2 - это синус 60°. Следовательно, в равнобедренном треугольнике углы при АВ=60°, ⇒ ∠АОВ=60°, а ∆ АОВ - равносторонний. Сторона данного многоугольника АВ=8. Угол АОВ - центральный, делит окружность на 360°:60°=6 равных углов, противолежащих каждой стороне многоугольника. ⇒ Данный многоугольник имеет 6 сторон.